本文介绍了训练后量化（PTQ）和量化感知训练（QAT）技术，PTQ 通过 Per-Tensor/Channel/Vector 等不同粒度划分量化参数，结合动态范围裁剪（校准集统计或 KL 散度优化）和 AdaRound 学习式舍入来平衡精度与效率；QAT 则在前向传播中模拟量化并利用直通估计器（STE）绕过梯度断层，而二元/三元量化通过引入可学习缩放因子减少极低比特（1-2bit）下的精度损失，在压缩模型的同时实现硬件加速与内存优化。

训练后量化 Post-training Quantization (PTQ)

量化粒度

  • Per-Tensor
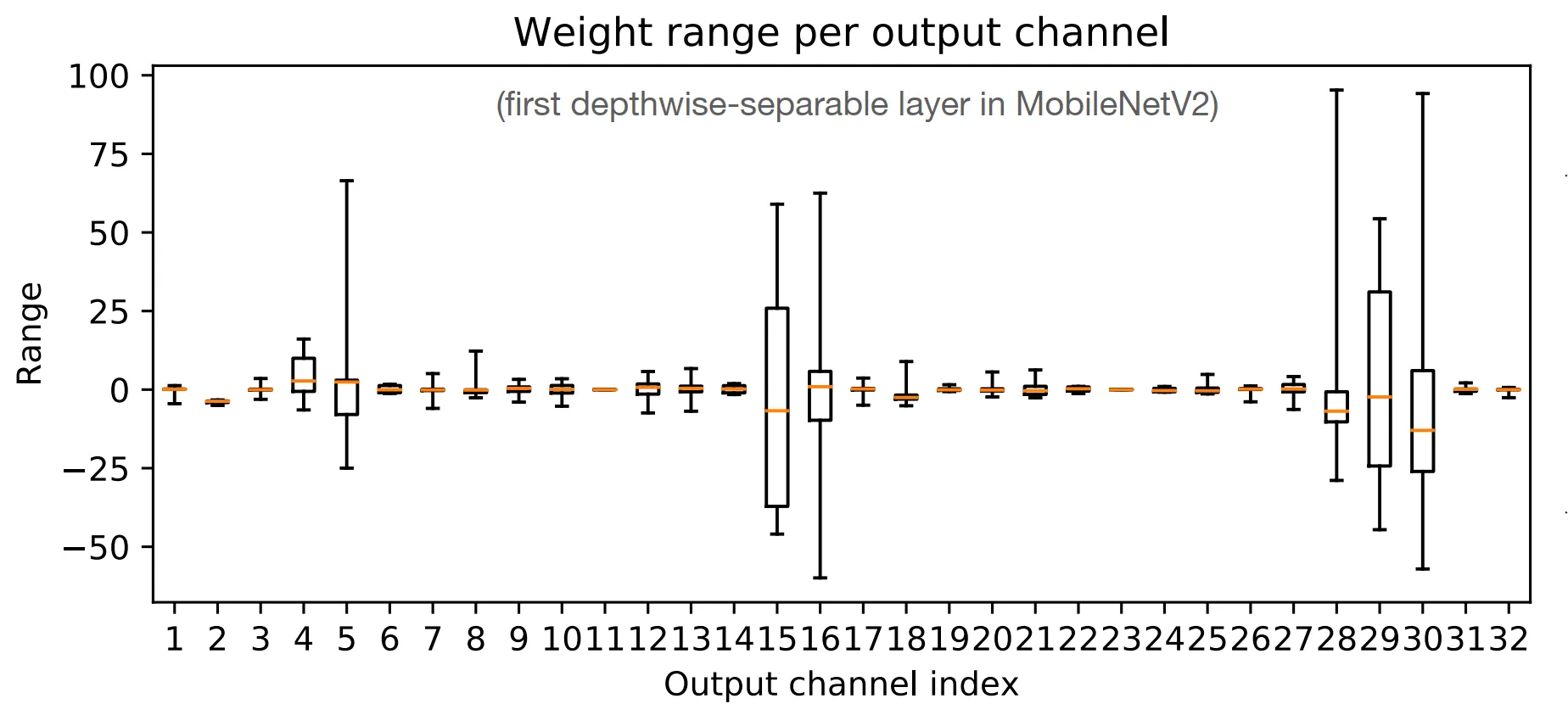
    整个张量共享一个缩放因子。对于一些小模型，精度损失得比较厉害。绘制出一个 Tensor 不同通道的箱式图，可以发现有的通道之间数据范围差异很大，因此不适合在 Tensor 尺度上使用统一的量化参数。

不同通道的箱式图

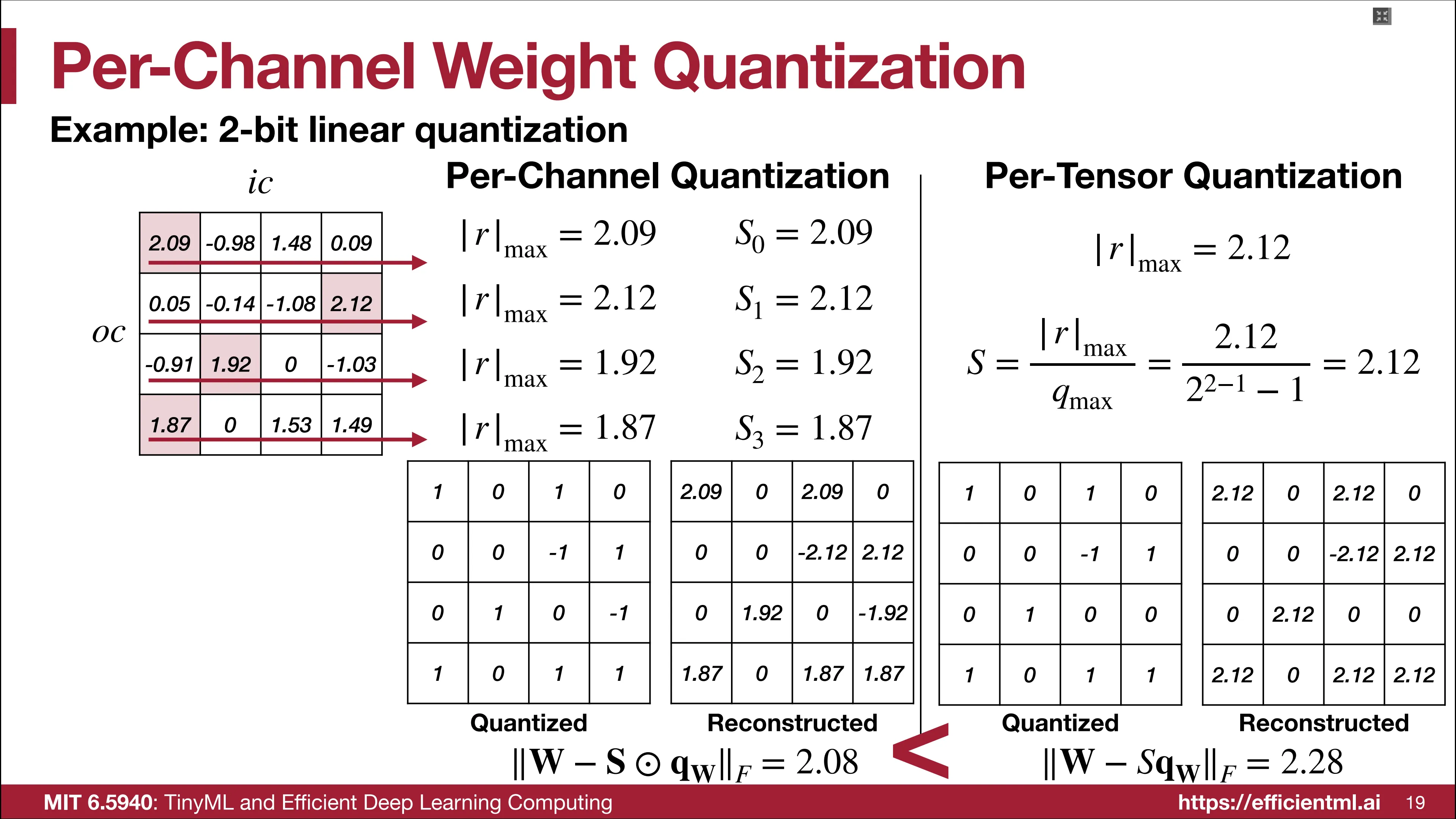
  • Per-Channel
    Per-Channel 为每个通道都计算了独立的放缩因子，该方案在反量化后能够得到更多样的权重表示，量化误差也相对应地更低。
    2 bit Per-Channel 线性量化示意图

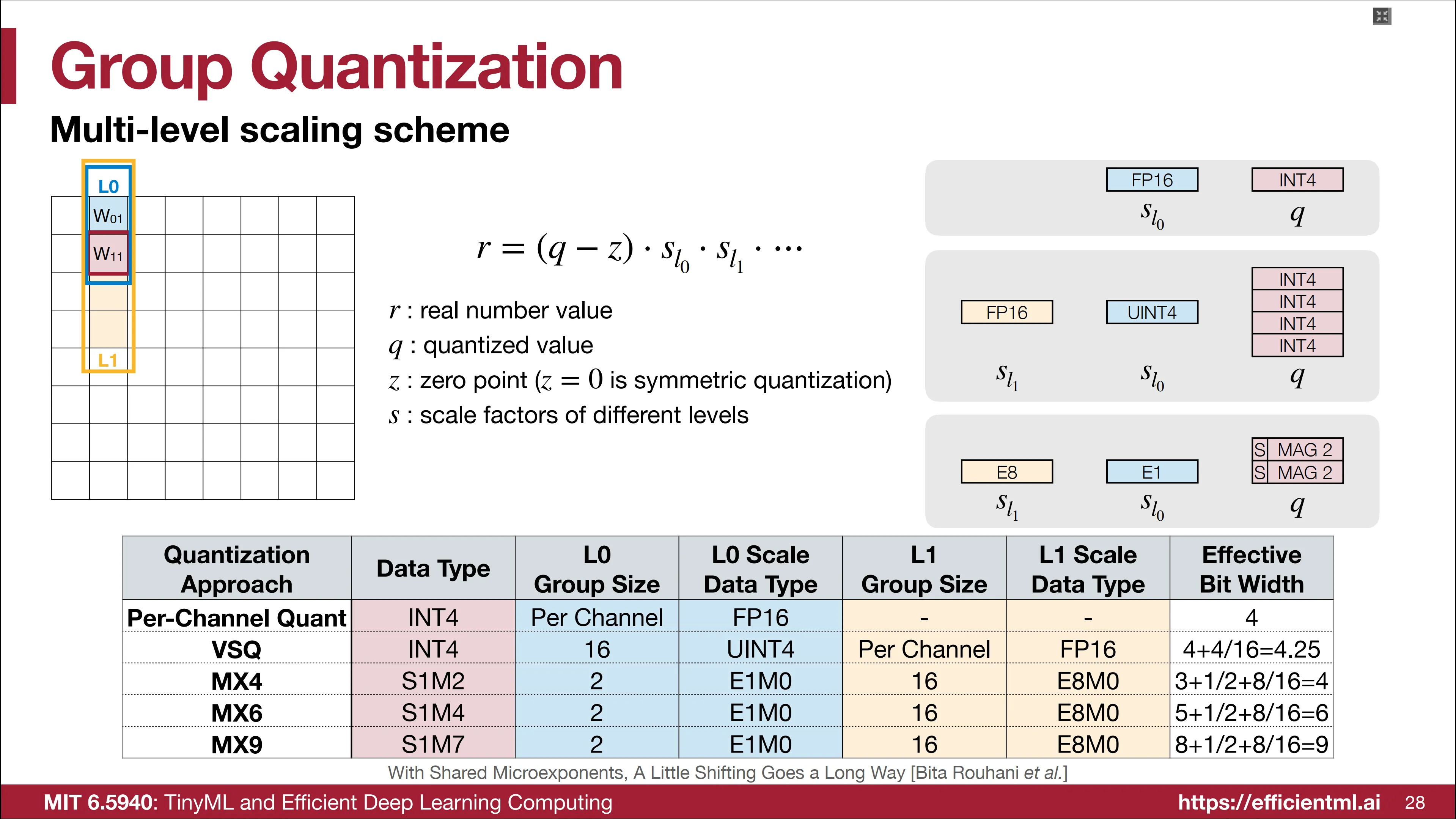
  • Group wise

Per-Vector在传统 Per-Tensor 量化的基础上，为每个子向量增加一个额外的整型缩放因子，即反量化公式变为：

$$ r=\gamma \cdot S_q(q-Z) $$

整个 Tensor 共享同一个高精度的缩放因子，达成了精度和硬件效率之间的折中。

以 4-bit quantization with 4-bit per-vector scale for every 16 elements 为例，实际的量化位宽为 4+4/16 = 4.25 bits。

Per-vector 本质上是一种多级的缩放方案，通过使用不同的数据表示类型来表示缩放因子，能够实现 MX4/6/9 等缩放方法，从而达成不同程度的量化位宽。
不同缩放方法汇总表

Dynamic Range Clipping

权重的数据在模型训练结束后就已经固定，因此其范围也是固定的。而激活层随输入数据的变化而变化，数据范围会很大，确定其数据范围的技术需要专门拿出来讨论。

首先需要收集激活层的统计信息，分为在训练过程中和训练后收集。

  • 训练时
    使用指数移动平均来统计训练过程中激活层的最大和最小值，其公式为：
$$ \hat{r}^{(t)}_{max,min} = \alpha \cdot r^{(t)}_{max,min}+(1-\alpha)\cdot \hat{r}^{(t-1)}_{max,min} $$
  • 训练后
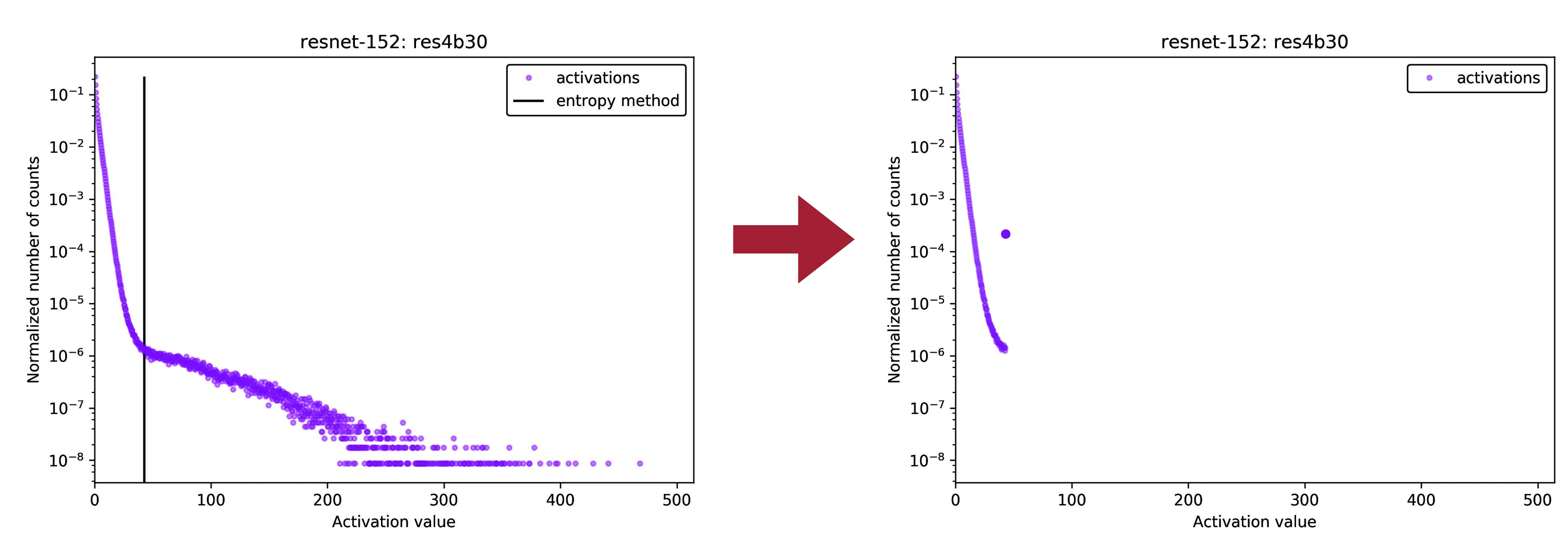
    如果无法获取训练时的数据集，可以在模型中运行一些校准集。激活层的数据分布可能如下图所示，两侧的长尾是激活层中的极值，这些极值的存在会降低量化范围的表示能力（通过压缩量化表示范围，可以在有限的数据位宽中提高量化的表示精度）。
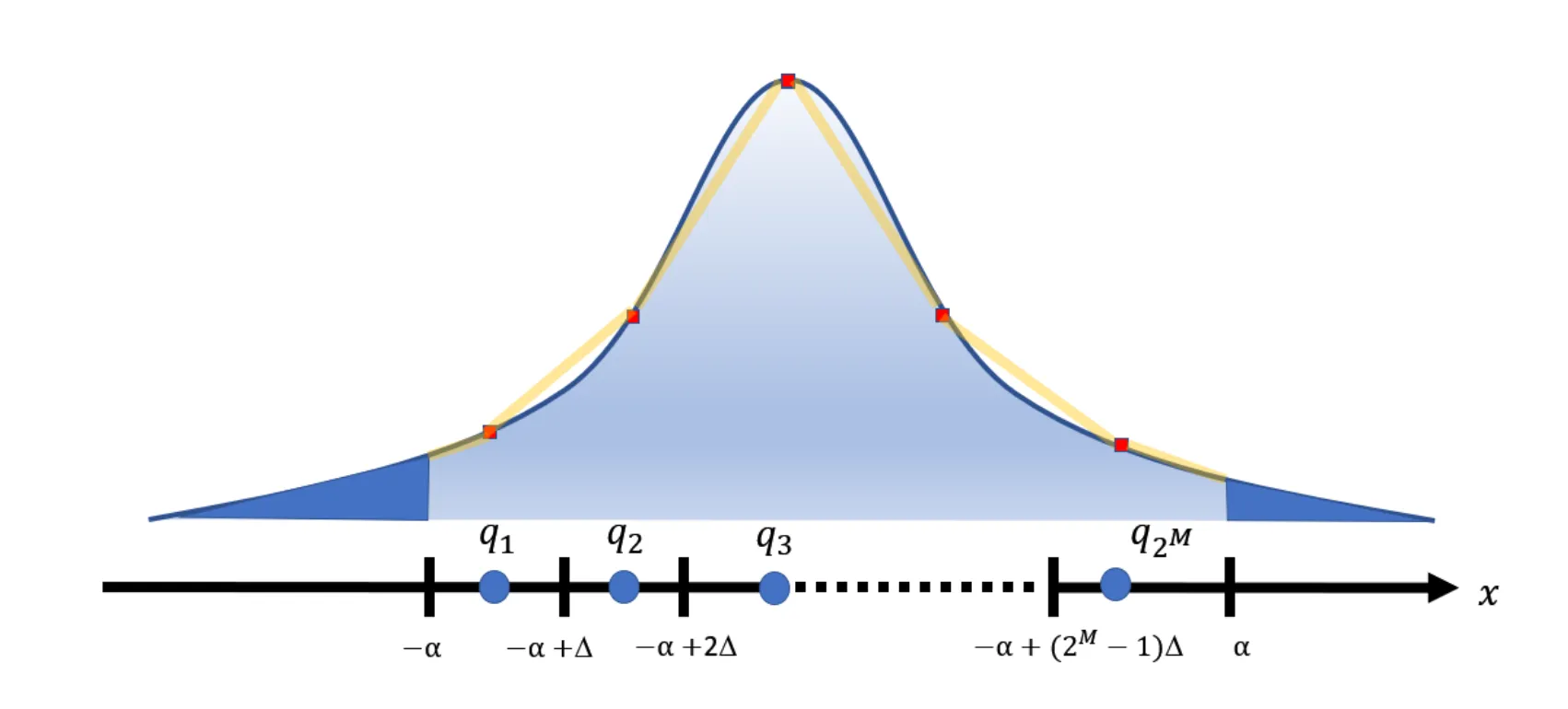
    激活层在校准集上的分布
    优化目标可以设置为最小化量化的均方误差，即：
$$ \min_{|r|_{\text{max}}} \mathbb{E} \left[ (X - Q(X))^2 \right] $$

对于高斯分布或者拉普拉斯等已知分布，可以求出上述优化目标的数值解。但对于一些不常见的分布，优化目标就是 KL 散度来衡量用量化后的分布来近似激活层的分布的信息损失，即：

$$ \min_{Q} D_{KL}(P || Q) = \min_{Q} \sum_{i=1}^{N} P(x_i) \log \frac{P(x_i)}{Q(x_i)} $$

最小化KL散度量化示意图

舍入

  • AdaRound
    常见的舍入策略是舍入到最近的数，例如四舍五入。但是很多时候这并不是一个最佳策略。这里介绍一种基于学习的舍入方法，在舍入前给张量加上一个可学习的参数再进行四舍五入，即：
$$ \tilde{w} = \mathrm{round}(\lfloor w \rfloor+\delta),\ \delta\in[0, 1] $$

那么确定该参数的优化目标为：

$$ \operatorname{argmin}_{V}\|Wx - \mathrm{round}(\lfloor W \rfloor+h(V))x\|_F^2 + \lambda f_{reg}(V) $$

其中，$V$ 为待学习参数，$h()$ 是一个将输入映射到 $[0, 1]$ 的函数，$f_{reg}$ 是一个正则项，使得 $V$ 接近于 0/1。

量化感知训练 Quantization-Aware Train (QAT)

在 K-means 量化中，将每个簇的梯度相加后作为该簇的梯度从而更新权重，线性量化的微调过程则要复杂得多。本节名字为 Quantization-Aware Train，即在训练过程中考虑量化。

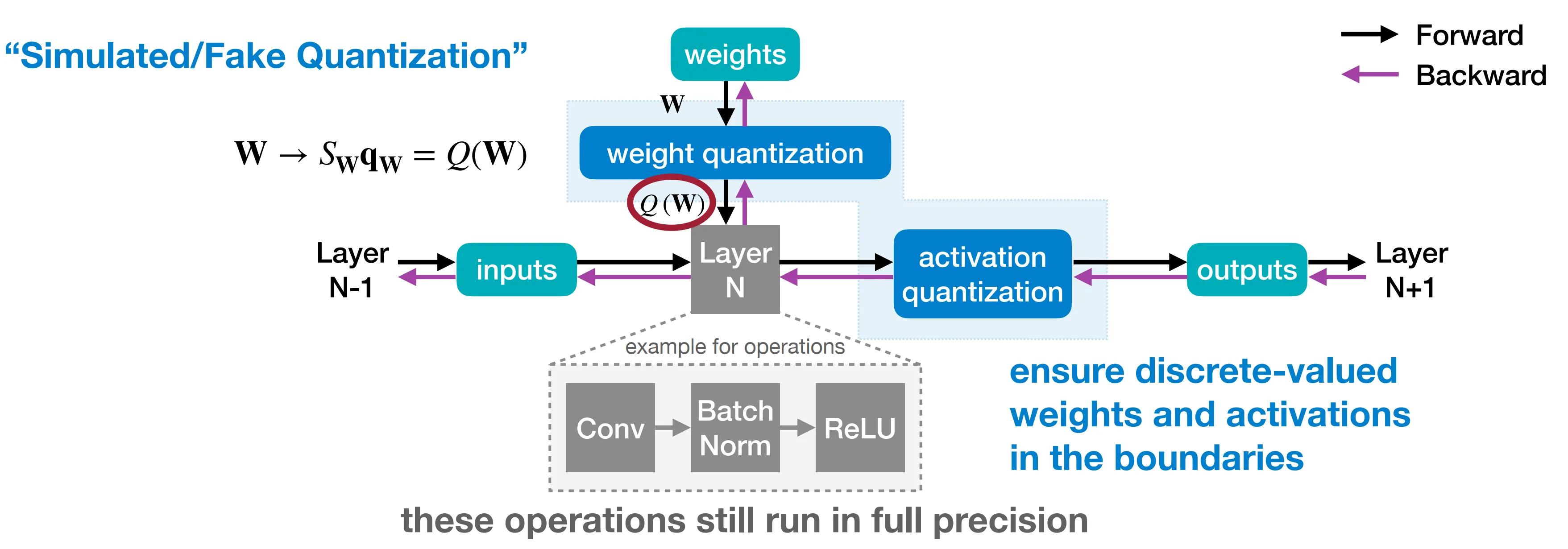
伪量化 Fake Quantization

伪量化示意图如下所示，在前向传播过程中对权重和激活层进行模拟量化（先量化到低精度，再反量化到高精度），再反向传播中使用高精度更新权重。
伪量化示意图

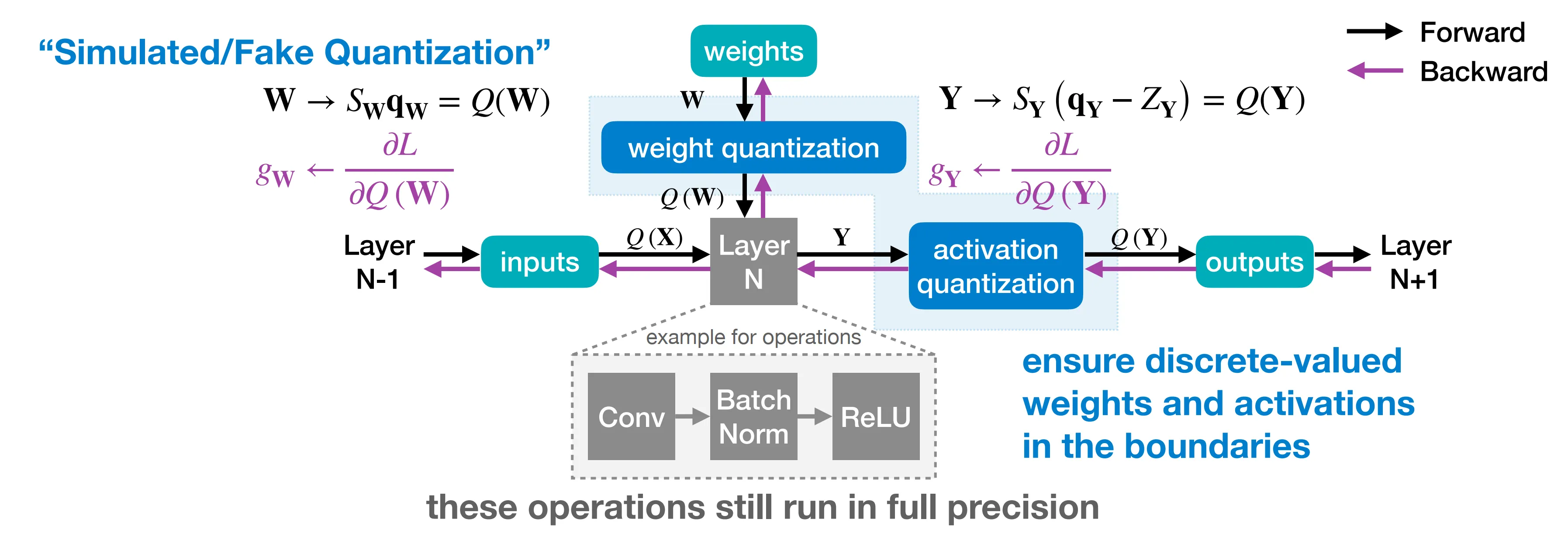
直通估计器 Straight-Through Estimator, STE

随之而来会引入一个新的问题，量化是一种舍入，这就导致输出层会变成分段的台阶函数，这个函数的梯度为 0。这里使用 STE 技术，绕过不可导的计算，即认为量化操作对梯度没有影响：

$$ \frac{\partial L}{\partial Q(x)} = \frac{\partial L}{\partial x} $$

加上 STE 后，整个 STE 的示意图如下所示，直接使用 Loss 对量化后的 W 和 Y 的梯度来估计对量化前的 W 和 Y 的梯度。
带有STE的伪量化示意图

二元/三元量化 Binary/Tenary Quantization

所谓二元/三元就是将权重量化到 0 和±1，从而大大减少内存占用和加速计算。

二元化

  • 确定性二元化
    确定性二元化根据一个阈值（常见为 0），小于该阈值的权重量化为 -1，大于该阈值的权重量化为 +1。可以预见的是，这个方案掉点很厉害。
  • 随机二元化
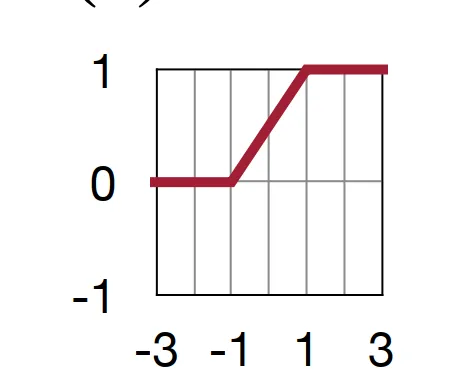
    一种随机策略为 Binary Connect，权重 r 以概率 $\sigma(\min (\max ((r+1)/2, 0), 1))$ 被量化到 1，否则量化到 -1，该函数的图像如下所示。简单来说，若权重大于 1 或者小于 -1，则被量化到 1 或者 -1，否则按照概率线性增加的形式量化到 1。
    hard sigmoid 函数图像
    这个方案的缺点是硬件不友好，其要求硬件在量化过程中生成随机数。

可以遇见的，采用这个方案量化后模型掉点很厉害，下图达到了 21.2%。但是，如果给量化后的权重增加一个 32 位的 scale factor，确保量化前后权重的均值一致，尽管量化误差仍旧很大，但是模型精度掉点仅仅只有 0.2。
二元量化示意图

同时二元量化权重和激活层

过于震惊，后面用到在学。

三元量化

  • Ternary Weight Networks, TWN
    三元量化将阈值之内的权重量化为 0，之外的量化为±1。阈值的选取一般为权重绝对值的均值乘上 0.7。同样这里需要一个 scale factor。
ImageNet Top-1 Acc. Full Precision 1 bit (BWN) 2 bit (TWN)
ResNet-18 69.6 60.8 65.3

符合预期得，三元量化精度损失小于二元量化。

  • Trained Ternary Quantization, TTQ
    为了进一步减少量化损失，TTQ 将量化后 scale factor 修改为两个可学习的参数，分别用来表示 +1 和 -1 对应的缩放系数，然后寻找这两个参数的最优值。