本讲开始介绍量化技术，首先介绍各种数据表示格式，然后介绍了两种量化技术：K-means和线性量化，最后提到了模型压缩的流水线。

数值数据类型

课程第一部分介绍了整型、定点小数、浮点数的数据表示格式，属于计算机组成原理的基本知识，此处不再赘述。

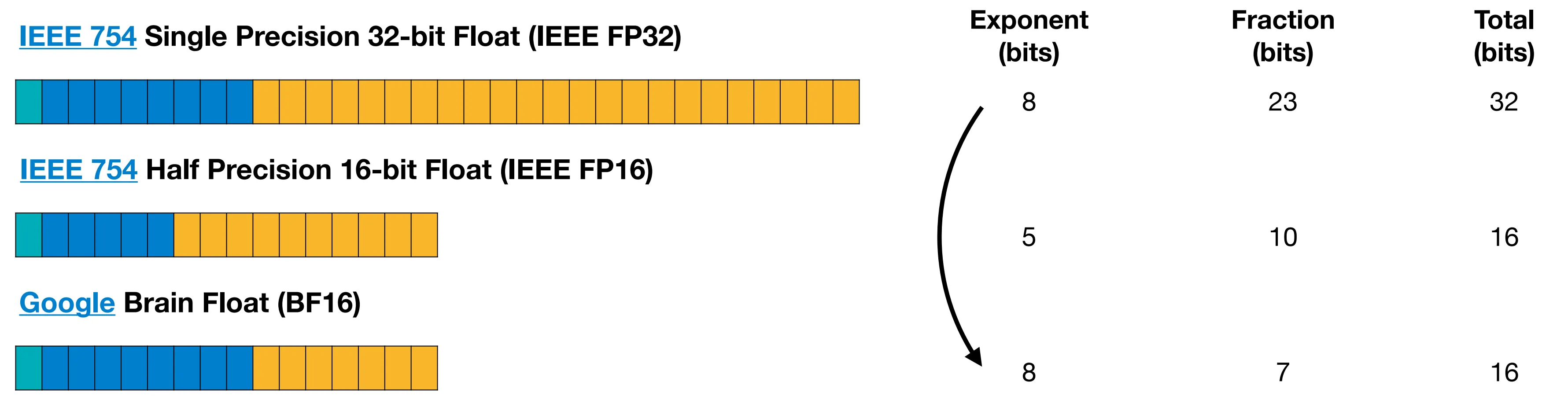
值得一提的是，在浮点数表示法中，阶码长度意味着该表示法能够表示数值的范围，尾数长度则决定该表示法能够表示的数据精度。如下图所示，Google 提出了一种 BF16 表示格式，其总共占用 2 字节，但是与 IEEE 754 格式中的 4 字节的单精度浮点数具有相同的阶码长度，从而对齐二者的表示范围。

NVIDIA 提出了两种不同的 8 位浮点数的表示格式，它们具有不同的阶数与尾数的长度：

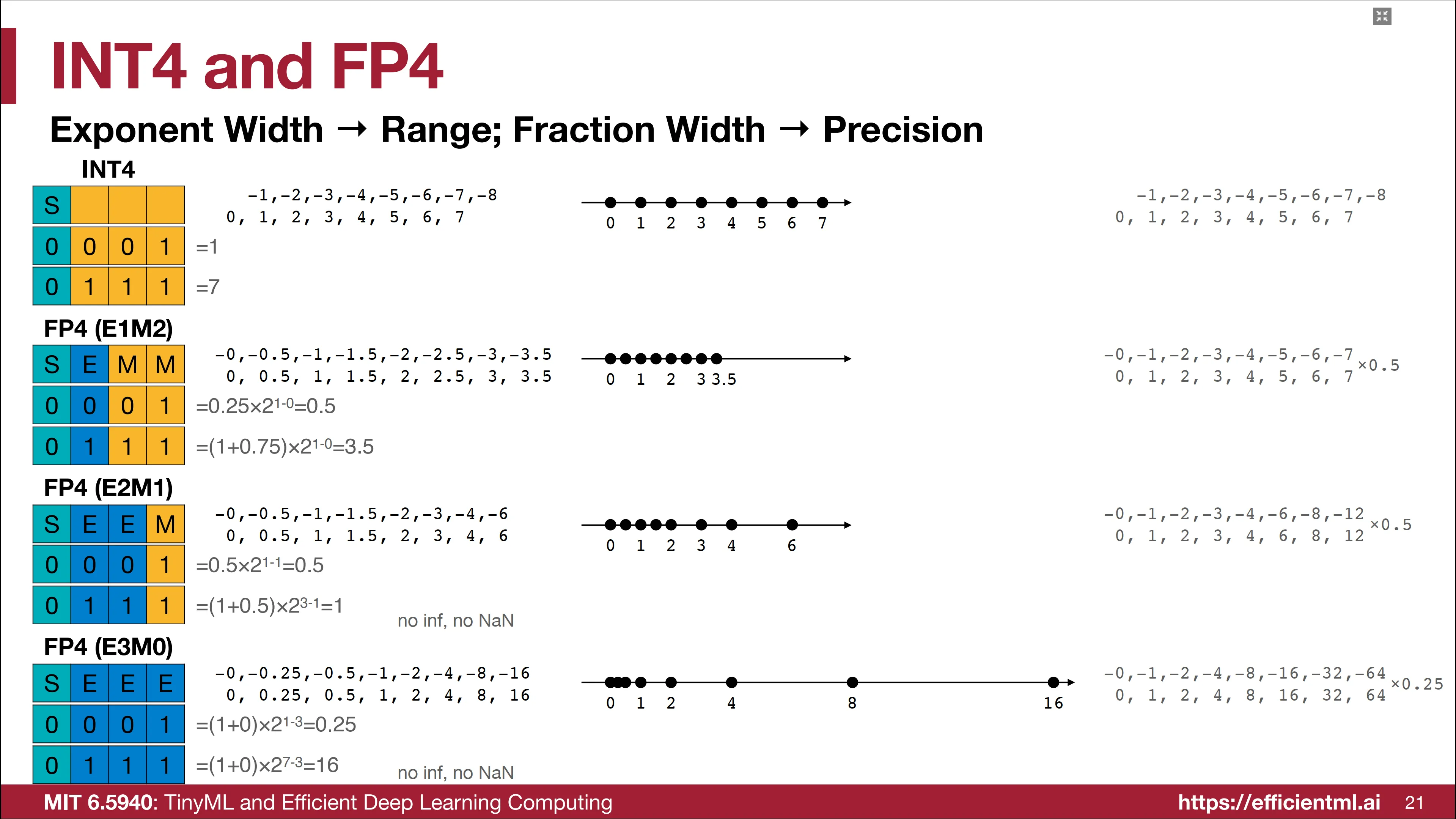
而如果仅仅使用 4 比特来表示整型或者浮点型，那能够表示出的数可以简单在数轴上点出：

量化

什么是量化

量化指的是将连续值或者大量的可能的离散取值近似为少量取值的过程。例如下图展示了对连续信号和对高清图片的量化效果。

量化前后的差别被定义为量化误差，量化过程需要最小化这一误差。

K-means 量化

如下图所示，基于 K-means 的量化算法通过 K-means 算法对所有权重进行聚类，每个权重使用其聚类后所在簇的簇中心值作为量化后的值，并在权重中使用簇号来指代。

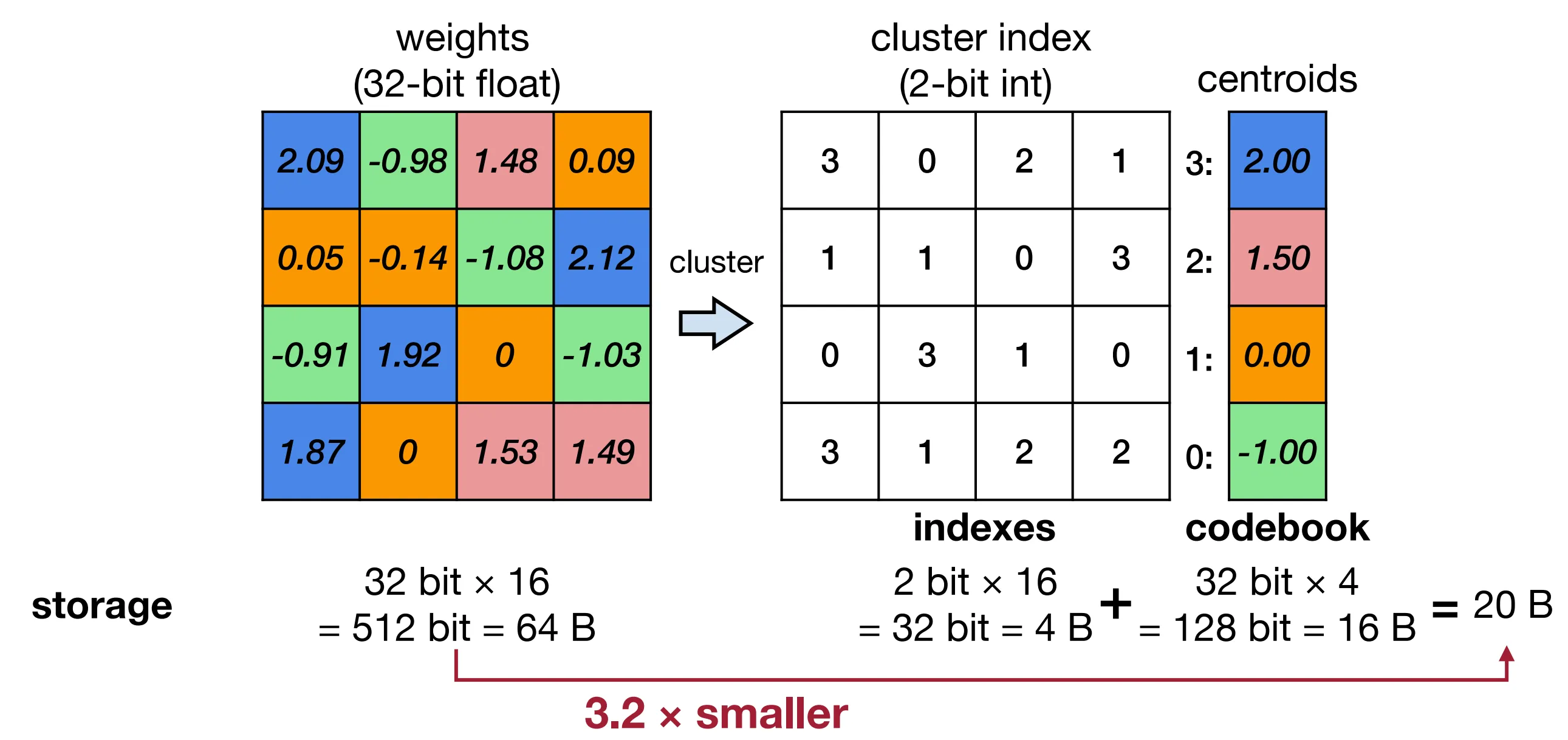
假设被量化为 $2^n$ 个簇，即每个权重需要使用 $n$ 比特整型表示其簇号，原始权重共有 $m$ 个参数，且 $m»2^n$。在量化前权重矩阵内存占用为 $32m$ 比特，量化后为 $nm+32\times 2^n$ 比特。考虑到 $m»2^n$，量化后近似为 $nm$ 比特，量化后内存相当于量化前的 $n/32$。

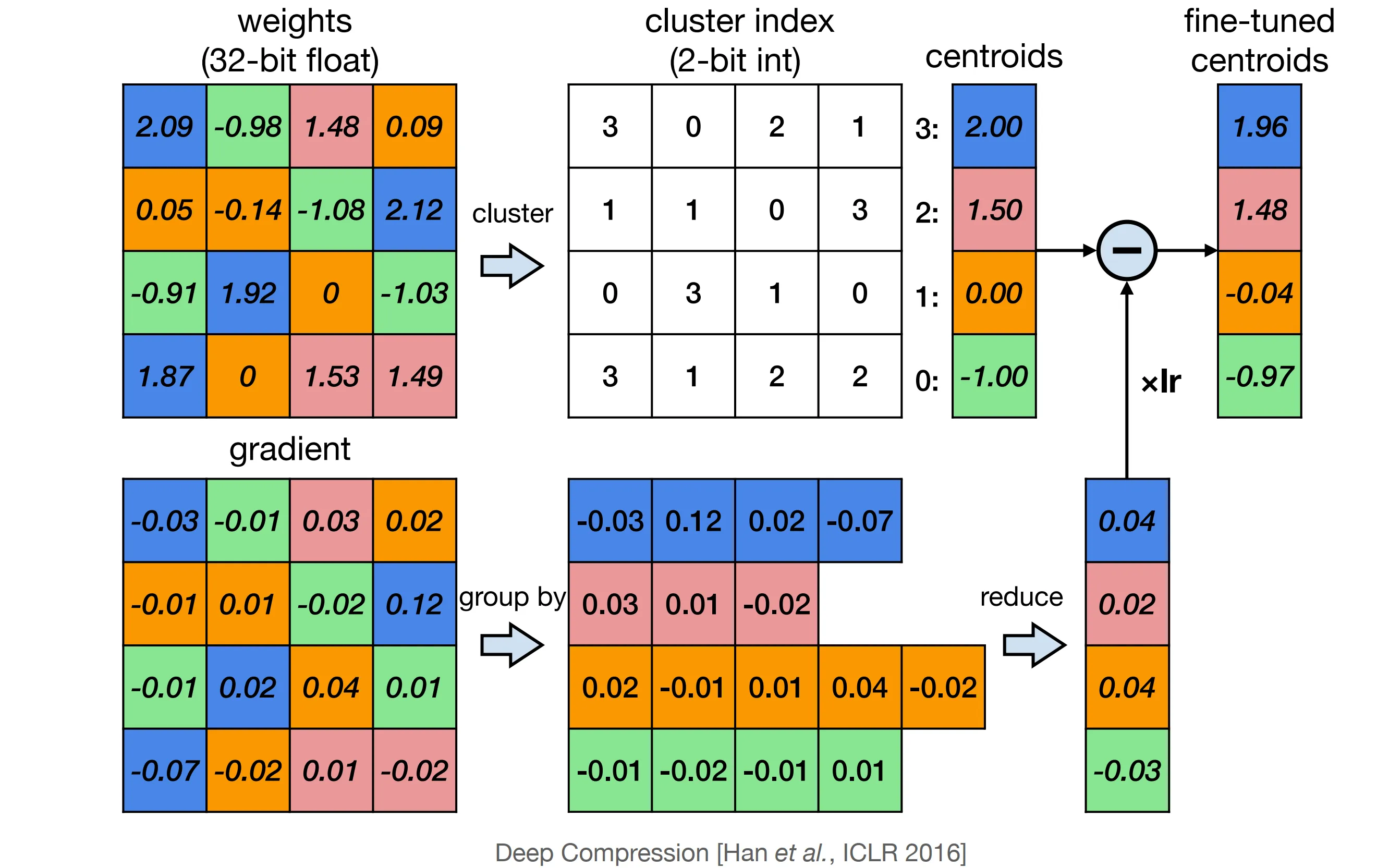
量化后的模型通过微调可以取的更好的效果，K-means 量化的微调算法将同一簇的梯度相加，作为这个簇共同的梯度，并进行权重更新。

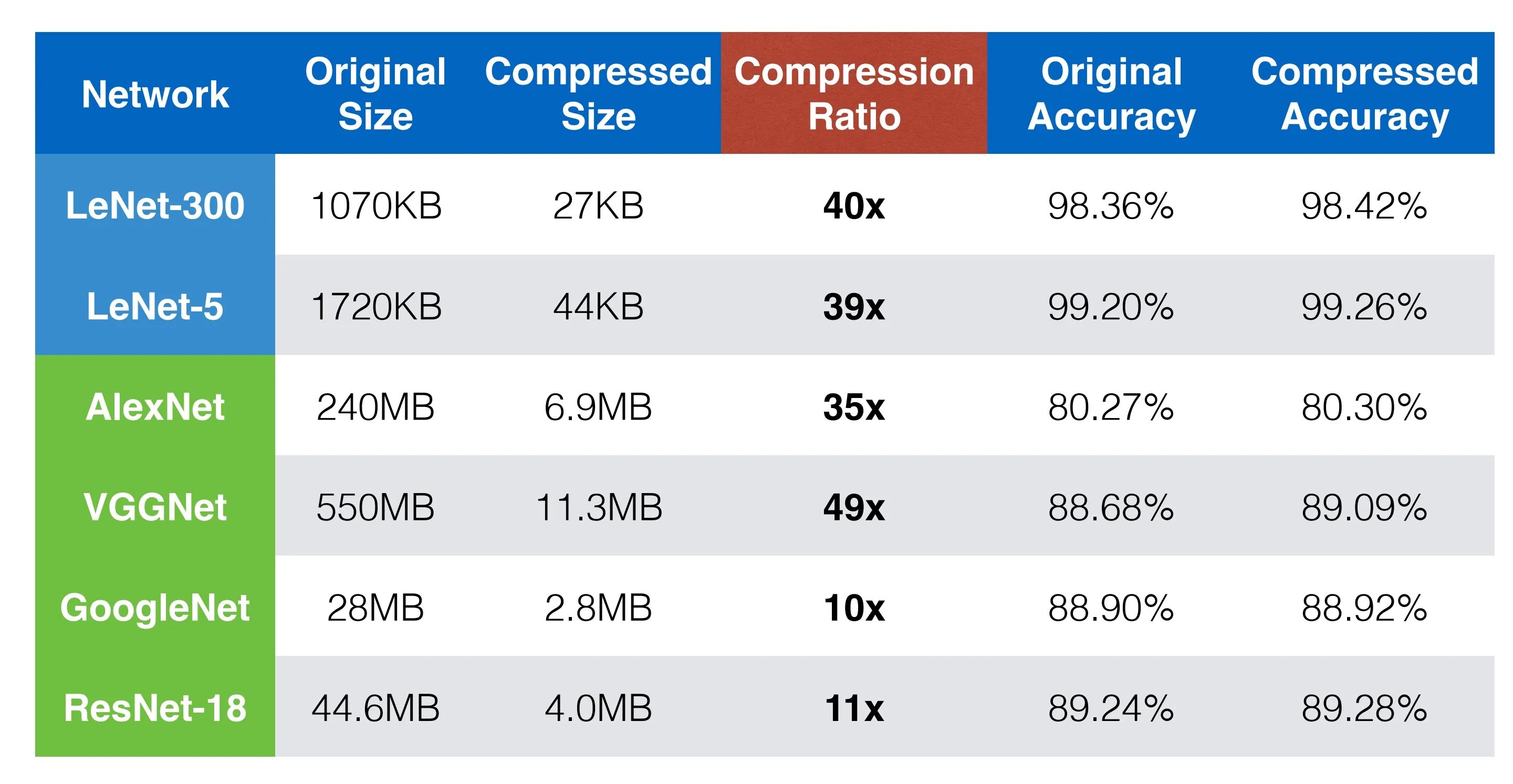
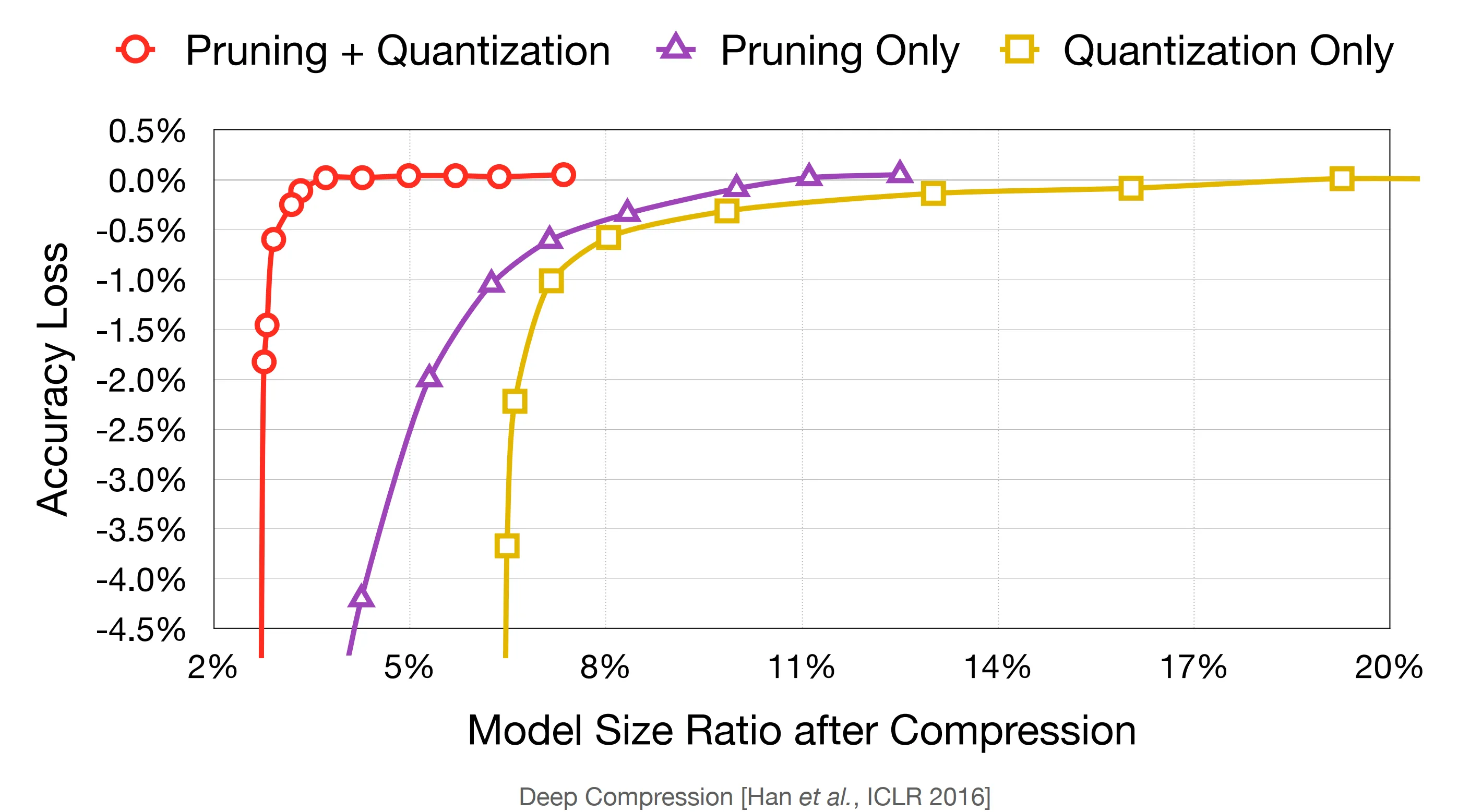
通过结合剪枝和量化两个策略，可以实现 20x 的模型压缩。

一般来说，先做剪枝，再进行量化。通过剪枝可以只保留有用的参数，减少量化的参数量。

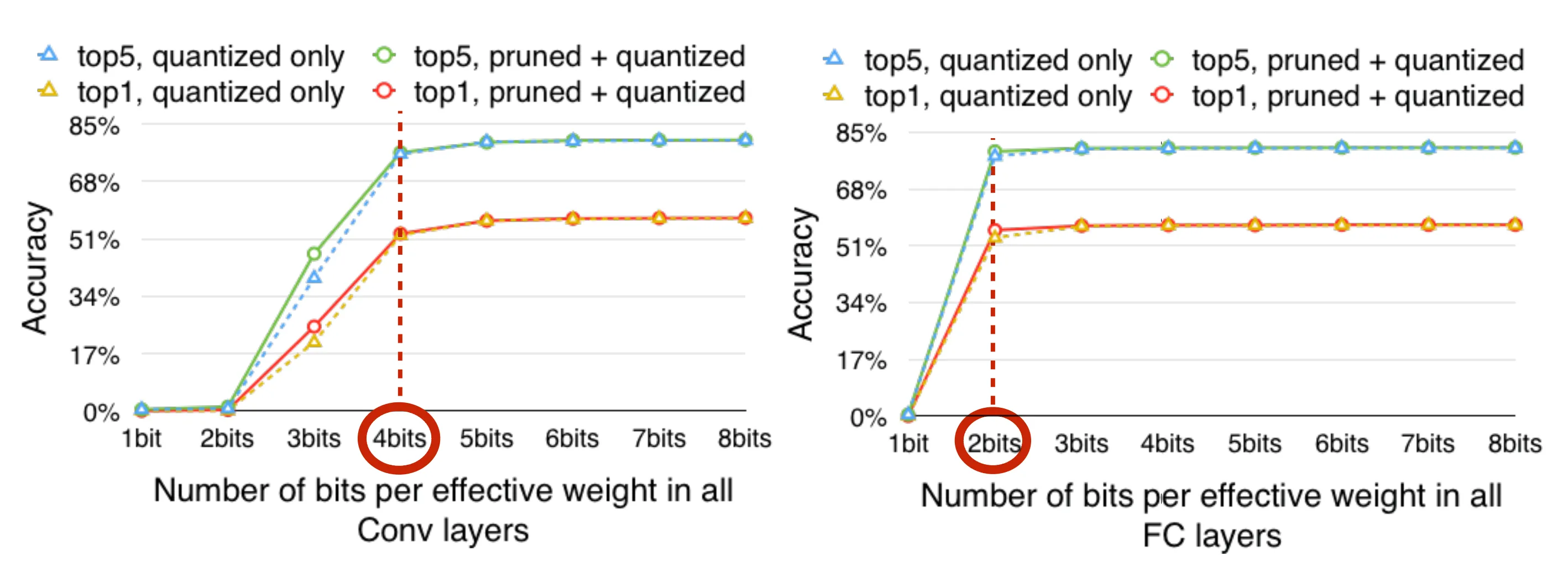
量化位宽一般取决于不同的模型，如下图所示，一般卷积层需要 4 比特，全连接层仅需要 2 比特。

此外，还可以使用哈夫曼编码来进一步压缩模型的大小，为频数高的参数使用较短的编码。

线性量化

线性量化利用了一种将低精度整型通过仿射变换转换为浮点数的技术，如下图通过仿射变换可以将量化后的 2 比特权重张量近似还原为原始权重张量。

上述变换中有两个参数需要确定，一个是整型参数零点 $Z$ 和一个浮点型参数放缩因数 $S$，放射变换过程可以使用公式表示为：

其中，q 为量化后权重矩阵的值，r 为经过还原后权重矩阵的值。其中，量化矩阵中恰好为 Z 的元素将被还原为 0，而 S 决定了还原后的范围。

记 $r^\prime$ 表示权重矩阵的真实值，那真实参数表示的范围为 $r_{max}^\prime-r_{min}^\prime$，而经过还原的参数表示范围为 $(q_{max}-q_{max})\times S$，让二者相等可以得到放缩因数的计算公式：

在课程中，计算 $Z$ 的方法是让原始矩阵和还原后的权重矩阵的最小值对齐，即 $r_{min}^\prime = (q_{min} - Z)\times S$，从而推导出零点的计算公式：

这里有点奇怪，为什么不是让整个权重矩阵的总误差最小。

使用线性量化计算矩乘

在矩乘计算 $\mathbf{Y} = \mathbf{WX}$ 中，三个矩阵均使用线性量化进行表示，通过恒等变换可以得到：

其中，与 $W$ 相关的变量都是常量，此外 $Z_W$ 也是常量（why???)，因此 $Z_X \mathbf{q_W} + Z_W Z_X$ 可以在量化时预先计算得到，在运行时没有计算开销。

对于放缩因子 $\frac{S_W S_X}{S_Y}$，经验上可以确定其范围在 $(0,1)$ 之间，因此，其可以表示为一个定点小数通过右移运算得到，如下图所示。因此只需要存储一个定点小数和右移次数，而不需要存储一个高精度浮点数。

考虑到权重一般是关于 0 对称，因此可以有理由假定 $Z_W=0$， 从而消去 $Z_W\mathbf{q_X}$ 和 $Z_W Z_X$ 这两项，从而计算公式变形为：

主要计算开销在于 $\mathbf{q_w q_x}$ 这一低精度整数矩乘计算。

模型压缩的流水线

模型压缩全流程如下所示，首先通过剪枝和微调来减少无效参数，然后通过量化来减少模型参数表示，最后使用哈夫曼编码进一步压缩模型大小。

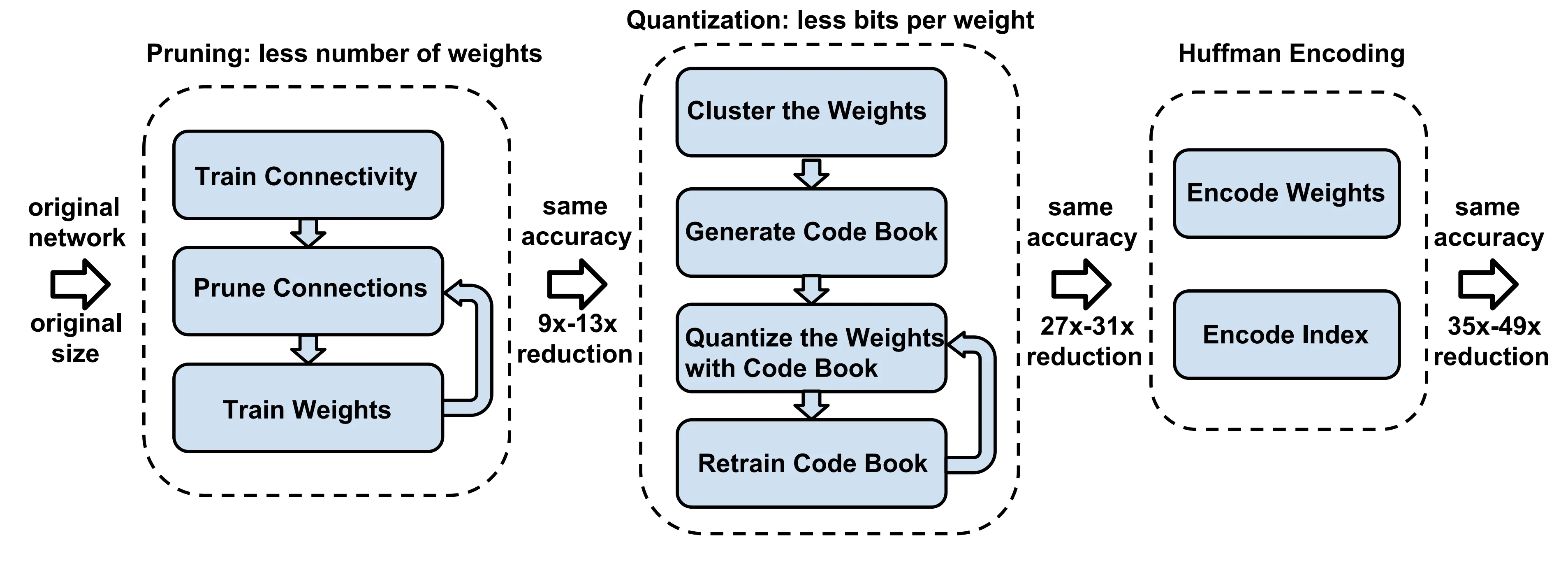
Again，在有着极高压缩率的同时，仍旧能够保持精度不变。