本讲延续上一讲继续介绍了两种确定剪枝比例的算法：灵敏度分析和强化学习。此外还介绍了为稀疏网络提供支持的硬件加速器，包括 EIE、NVIDIA Tensor Core、TorchSparse 等。

如无另外说明，图片均引用自 EfficientML 课程幻灯片。

Lecture 4: Pruning and sparsity 剪枝和稀疏性

剪枝率

如下图所示，研究指出对每一层采取不均匀的剪枝比例的效果显著优于均匀剪枝，问题在于如何确定每一层的剪枝比例。

灵敏度分析

通过对每一层灵敏度进行分析，即对每一层按照不同剪枝率进行剪枝，观察其对最后精度的镜像程度来判断精度对于每一层的敏感程度。如下图所示，可以发现精度对于 L1 层最不敏感，对于 L0 层最敏感。

此外，当我们实现剪枝算法时，灵敏度曲线也可以用于检查算法是否实现有误：前期几乎不掉点，后期显著掉点。

进行灵敏度分析之后，可以确定一个能够接受的掉点阈值，根据此阈值确定每一层的剪枝比例。

这里隐含了一个假设：这些层之间是相互独立的，即我们没有考虑层一层之间的交互作用。

自动剪枝

之前聊过的剪枝方案都是由人工来确定剪枝策略的，但是这种方案不够优雅，并且不具备可扩展性 (scalability)。

这里介绍一种基于强化学习的剪枝比例确定方案，其动机是我们训练一个模型，输入为每一层的信息，输入为相对应的剪枝比例。

笔者缺乏强化学习领域相关知识，以下翻译可能不太恰当。

我们的模型 setup 为：

• 状态（输入）
  • 描述每一层的特征，包括层序号、通道数、卷积核大小、FLOPs…
• Action （应该是模型输出？）
  • 0 到 1 之间的数，表示剪枝率
• 智能体
  • DDPG agent（不懂）
• 奖励 （目标函数？）
  • -Error 如果满足约束
  • -inf 如果不满足

如下图所示，相比人类耗时地手工调优，基于强化学习的方法耗时更短并且性能更优。

微调剪枝后的神经网络

前文提到，剪枝完成后需要对网络进行微调，以恢复网络性能或者取得更好的效果。

• 学习率：一般设置为原先学习率的十分之一到百分之一
• 采用迭代剪枝：第二讲提到对迭代进行剪枝 - 微调的效果显著优于一次性的剪枝 - 微调操作
• 正则化：在微调过程中需要使用 L1 或者 L2 正则化

为稀疏性提供支持的系统

EIE: Efficient Inference Engine

EIE 使用了三种优化方式：

• 权重稀疏化：能够节省 90% 的计算资源和 80% 的内存资源，内存节省略少是由于保存稀疏信息带来的额外开销
• 激活层稀疏化：能够节省 66% 的计算资源
• 量化

对于如上的稀疏矩阵 - 向量乘法 (Sparse Matrix Vector Multiplication, SpMV)，上半图表示 SpMV 的逻辑形式，权重矩阵被染为四种颜色，每个颜色代表一个处理单元 PE 即 processing element，这些 PEs 将并行执行。下半图表示第一个 PE 中保存的权重信息，PE0 中的稀疏矩阵采取的是 CSC 格式 ¹，即在内存中 Virtual Weight 只保存 5 个非零元素，以及这五个非零元素与前一个非零元素之间的距离 Relative Index【这里是列优先的距离】，和指向列的行指针 Column Pointer。Pointer[i] 表示从 Virtual Weight 中第 Pointer[i] 开始是原稀疏矩阵中第 i 行的元素。

注意，上图并非标准 CSC 格式，在标准格式中，采用的 Row Index 来直接记录行号，而非使用 relative Index 记录相邻元素之间的距离。

在计算过程中，每个 PE 对输入向量 $\vec{a}$ 逐元素遍历，直接跳过零元；对于非零元素，将其广播到所有非零元 PE 中并计算想用结果。

整个 PE 单元的微架构图如下所示：

首先是 Activation Queue 用于存储所有非零激活层元素，然后根据非零元的 Activation Index 来获取 Weight Column Pointer，确定与激活层元素相对应的权重元素的起始和结束索引，接着获取权重元素，并对其进行解码（解码相关将在后文说明），最后将结果暂存累加，并经过 ReLU 层后输出。

得益于激活层和权重矩阵的稀疏性，可以将其放在 SRAM 中加速存取。

NVIDIA Tensor Core

第三讲提到的 M:N 的稀疏策略，即连续 N 个元素中必定有 M 个零元素。例如，2:4 的稀疏矩阵可以表示为：

对于 2:4 的且形状为 RxC 的稀疏矩阵，在内存中可以只保存所有非零元，即 R x C/2 的矩阵。还需要保存额外的元数据来确定非零元在原始矩阵中的位置，每个非零元可能来自其原来小组的 0~3 中的某个位置，因此每个非零元需要 4 bit 信息来记录其在小组中的原始位置。

上图右侧展示了 Tensor core 中稀疏矩乘的实现，以 A 的第一行为例，A 的第一行需要与 B 的第一列做内积，使用 A 在稀疏化过程中保存的 indices 信息，就可以对 B 的第一列进行筛选，只索引出 A 中非零元对应位置的元素，并进行乘法和累加操作。

TorchSparse

这里介绍一种稀疏卷积：如下图左所示，当对稀疏矩阵进行传统卷积操作时，经过卷积后激活层的稀疏度会下降，非零元素会逐渐扩散到周围的零元中；而在右侧的稀疏卷积中，要求保持输入中的稀疏性，即卷积后的零元仍旧是零元。

在稀疏卷积的实现中，对于单次卷积，只有非零元参加与卷积核的矩乘计算。这里介绍的实现方式为：建立输入元素 - 输出元素 - 卷积核权重的三元组，按照权重对三元组进行排序（实质上找到所有需要与该权重做乘法的元素）。

分组结束后，就可以采用一种自适应分组算法将上述标量乘法 - 加法转换为矩阵乘法（这一转换过程我直觉上认为类似于 img2col 技术将卷积转换为矩乘）。当然，这一过程存在大量开销。

• 计算规律性 (computation regularity) 与计算开销之间的折中
  为了将多个向量乘法聚合为一个矩阵乘法，我们不得不对某些较短的向量进行补零操作，这使得计算过程呈现出更好的规律性，但是带来了额外的计算开销。如下图所示，这里采取的折中手段是对每个计算 batch 进行动态分组
  

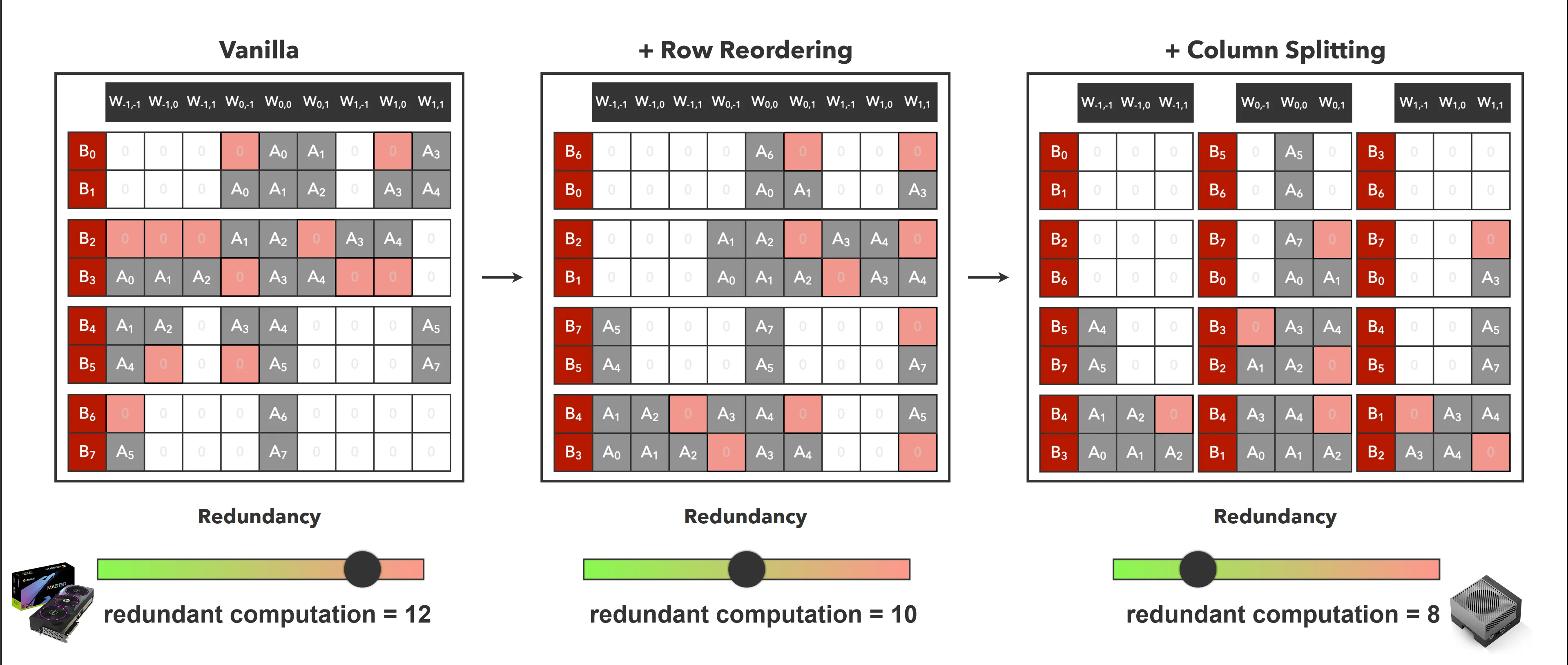
TorchSparse++

如下图左所示，邻接的行在一组中进行计算，以第一行为例，为了计算出 B1，在计算 B0 中必须将 $W_{0,-1}$ 和 $W_{1,0}$ 也参与计算，这就是前文提到的额外计算开销。在 TorchSparse++ 中，提出了一种行重排算法，经过重新分组后可以减少此类冗余计算。此外，还可以对权重进行分割，以实现更加细粒度的冗余优化。

PointAcc: 稀疏卷积的硬件加速器

这里介绍了前面一直在用的“输入元素 - 输出元素 - 卷积核权重”三元组的构建算法，该算法可以使用硬件加速，但没太理解算法原理，似乎也不是重点，略。

参考