写在最前面

从 2024-04-28 到 2024-09-08，历时四个多月，总算把 DLSys 学完了。这门课的一些收获：

  • 自动微分理论知识和在实践过程中衍生的包括计算图等知识
  • 系统学习了 ML 中几个基本模型和组件
  • Tensor 的 strides 相关内容
  • 基础 CUDA 编程

个人认为这门课一些没达到我预期的地方：

  • CUDA 编程的内容太浅
  • 后续讲 CNN、RNN、Transformer 的部分没必要，可以继续深入 CUDA 或者压缩课时

本门课程的核心内容在 Lecture 0~15，对应的 homework 是 hw0~3，后面的内容没有时间可以跳过。

ps：全文章两万余字，Chrome 渲染图片时可能会很卡，建议使用 Microsoft Edge 浏览。

Lecture 1: Introduction and Logistics

课程的目标

本课程的目标是学习现代深度学习系统，了解包括自动微分、神经网络架构、优化以及 GPU 上的高效操作在内的技术的底层原理。作为实践，本课程将实现一个 needle（deep learning library）库，类似 PyTorch。

为什么学习深度学习系统？

为什么学习？深度学习这一概念很早就存在了，但直到 PyTorch、TensorFlow 此类现代深度学习框架发布，深度学习才开始迅速发展。简单易用的自动差分库是深度学习发展的最大动力。

除了使用这些库，我们为什么还要学习深度学习系统？

  • 为了构建深度学习系统
    如果想要从事深度学习系统的开发，那毫无疑问得先学习它。目前深度学习框架并没完全成熟，还有很多开发新功能，乃至新的框架的机会。

  • 为了能够更高效地使用现有系统
    了解现有系统的内部实现，可以帮助我们写出更加高效的深度学习代码。如果想要提高自定义算子的效率，那必须先了解相关操作是如何实现的。

  • 深度学习系统本身就很有趣
    尽管这个系统看上去很复杂，但是其核心算法的原理确实相当简单的。两千行左右的代码，就可以写出一个深度学习库。

预备知识

  • systems programming
  • 线性代数
  • 其他数学知识：计算、概率、简单的证明
  • Python 和 C++ 经验
  • 机器学习的相关经验

Lecture 2: ML Refresher & Softmax Regression

机器学习基础

深度学习是由数据驱动的，所谓数据驱动，这意味着当我们想要写一个用于识别手写数字的模型时，我们关注的不是某个数字形状上有什么特点，如何通过编程识别该特点，而是直接将数据集喂给模型，模型自动训练并识别数字类别。

深度学习模型由三部分组成：

  • 假说模型：模型的结构，包括一系列参数，其描述了模型从输入到输出的映射关系；
  • 损失函数：指定了对模型的评价，损失函数值越小，说明该模型在指定任务上完成得更好；
  • 优化方法：用于对模型中参数进行优化，使得损失函数最小的方法。

Softmax 回归

以经典的 softmax 回归模型为例，简单回顾一下 ML 模型。

考虑一个 k 分类任务，其中数据集为 $x^{(i)} \in R^n\ ,\ y^{(i)} \in { 1,…,k}\ \ \ i = 1,…,m$，$n$ 标识输入数据集的维度，$k$ 标识标签类别数，$m$ 标识数据集样本数量。

一个假说模型就是将一个 $n$ 维的输入映射到一个 $k$ 维的输出，即：$h: R^n \rightarrow R^k$。注意，模型并不会直接输出类别的序号，而是通过输出一个 $k$ 维向量 $h(x)$，其中第 $i$ 个元素 $h_i(x)$ 表示是第 $i$ 个类别的概率。

对于线性模型来说，使用 $\theta \in R^{n\times k}$ 这个模型中的参数，那么 $h_\theta(x) = \theta^T x$。

如果一次输入多个数据，那么输入数据就可以组织成一个矩阵，相比起多个向量操作，矩阵的操作通常效率更高，我们在代码实现中一般也是用矩阵操作。数据集可以表示为：

$$ X\in R^{m\times n}=\left[ \begin{array}{c} x^{(1)T}\\ \vdots\\ x^{\left( m \right) T}\\ \end{array} \right] , y\in \left\{ 1,...,k \right\} ^m=\left[ \begin{array}{c} y^{\left( 1 \right)}\\ \vdots\\ y^{\left( m \right)}\\ \end{array} \right] $$

数据集的矩阵是一个个样本转置后堆叠 stack 起来的。那么输出可以表示为：

$$ h_{\theta}\left( X \right) =\left[ \begin{array}{c} h_{\theta}\left( x^{\left( 1 \right)} \right) ^T\\ \vdots\\ h_{\theta}\left( x^{\left( m \right)} \right) ^T\\ \end{array} \right] =\left[ \begin{array}{c} x^{\left( 1 \right) T}\theta\\ \vdots\\ x^{\left( m \right) T}\theta\\ \end{array} \right] =X\theta $$

关于损失函数 $l_{err}$，一种朴素的想法是将模型预测错误的模型数据量作为损失函数，即如果模型预测的正确率最高的那个类别与真实类别不相同，则损失函数为 1，否则为 0：

$$ l_{err}\left( h\left( x \right) , y \right) \,\,=\,\,\left\{ \begin{align*} 0 \ &\mathrm{if} \ \mathrm{argmax} _i\,\,h_i\left( x \right) =y\\ 1 \ &\mathrm{otherwise}\\ \end{align*} \right. $$

遗憾的是，这个符合直觉函数是不可微分的，难以对参数进行优化。更合适的做法是使用交叉熵损失函数。

在此之前，我们将先讲输出过一个 softmax 函数，使之的行为更像一个概率——各个类别的概率之和为 1：

$$ z_i=p\left( \mathrm{label}=i \right) =\frac{\exp \left( h_i\left( x \right) \right)}{\sum_{j=1}^k{\exp \left( h_j\left( x \right) \right)}} $$

那么交叉熵损失函数就可以定义为：

$$ l_{ce}\left( h\left( x \right) ,y \right) =-\log p\left( \mathrm{label}=y \right) =-h_y\left( x \right) +\log \sum_{j=1}^k{\exp \left( h_j\left( x \right) \right)} $$

注意在计算交叉熵时，通过运算进行了化简，这使得我们可以省去计算 softmax 的过程，直接计算最终的结果。不但如此，交叉熵的计算中，如果 $h_i(x)$ 的值很小，那么取对数会出现很大的值，化简后的计算则避免了这种情况。

所有的深度学习问题，都可以归结为一下这个最优化问题：

$$ \mathop {\mathrm{minimize}} \limits_{\theta}\ \ \frac{1}{m}\sum_{i=1}^m{l(h_{\theta}(x^{(i)}),y^{(i)}))} $$
我们使用梯度下降法对该问题进行优化。在此之前，首先介绍一下关于梯度。我们的优化目标可以看作一个关于$\theta \in R^{n\times k}$的函数$f$，那么其在$\theta_0$处的梯度可以表示为：
$$ \nabla _{\theta}f\left( \theta _0 \right) \in R^{n\times k}=\left[ \begin{matrix} \frac{\partial f\left( \theta _0 \right)}{\partial \theta _{11}}& \cdots& \frac{\partial f\left( \theta _0 \right)}{\partial \theta _{k1}}\\ \vdots& \ddots& \vdots\\ \frac{\partial f\left( \theta _0 \right)}{\partial \theta _{n1}}& \cdots& \frac{\partial f\left( \theta _0 \right)}{\partial \theta _{nk}}\\ \end{matrix} \right] $$
其中，第$i$行第$j$个元素表示除$\theta_{ij}$之外的参数都被当作常数，对$\theta_{ij}$求偏导。

梯度下降，就是沿着梯度方向不断进行迭代，以求找到最佳的$\theta$使得目标函数值最小。

$$ \theta :=\theta _0-\alpha \nabla f\left( \theta _0 \right) $$
上式中，$\alpha$被称为学习率或者步长。

事实上，在现代深度学习中，并不是使用的传统梯度下降的方案，因为其无法将所有训练集一次性读入并计算梯度。现代使用的是随机梯度下降（Stochastic Gradient Descent，SGD）

首先将m个训练集样本划分一个个小batch，每个batch都有B条数据。那每一batch的数据表示为$X\in R^{B\times n}$，更新参数$\theta$的公式变为：

$$ \theta :=\theta _0-\frac{\alpha}{B}\nabla f\left( \theta _0 \right) $$
我们的梯度变成了每个小batch对全体样本梯度的估计。

那如何计算梯度表达式呢？梯度矩阵中每个元素都是一个偏导数，我们就先从计算偏导数开始。假设$h$是个向量，我们来计算偏导数$\frac{\partial l_{ce}\left( h,y \right)}{\partial h_i}$：

$$ \begin{align*} \frac{\partial l_{ce}\left( h,y \right)}{\partial h_i}&=\frac{\partial}{\partial h_i}\left( -h_y+\log \sum_{j=1}^k{\exp h_j} \right) \\ &=-1\left\{ i=y \right\} +\frac{\exp \left( h_j \right)}{\sum_{j=1}^k{\exp h_j}} \\ &=-1\left\{ i=y \right\} +\mathrm{softmax} \left( h \right) \\ &=z-e_y \end{align*} $$

如果$h$是个向量，那么梯度$\nabla_h l_{ce}(h,y)$就能够以向量的形式表示为：

$$ \nabla_h l_{ce}(h,y) = z-e_y $$
这里我们将对$h$进行softmax标准化记为$z$，$e_y$表示对应的单位向量。

事实上，我们要计算的梯度是关于$\theta$的，具体来说，表达式为$\nabla_\theta l_{ce}(\theta^Tx,y)$，其中，$\theta$是个矩阵。或许，可以使用链式法则进行求解，但是太麻烦了，这里还涉及矩阵对向量的求导。我们需要一种更加通用的求导方案。

有两个解决办法：

  • 正确且官方的做法：使用矩阵微分学、雅可比矩阵、克罗内克积和向量化等知识进行求解。
  • 一个hacky、登不上台面、但大家都在用的方案：将所有的矩阵和向量当作标量，使用链式法则求解，并进行转置操作使得结果的size符合预期，最后检查数值上结果是否正确。

按照第二个方法的逻辑，过程为：

$$ \begin{align*} \frac{\partial}{\partial \theta}l_{ce}\left( \theta ^Tx,y \right) &=\frac{\partial l_{ce}\left( \theta ^Tx,y \right)}{\partial \theta ^Tx}\cdot \frac{\partial \theta ^Tx}{\partial \theta} \\ &=\left[ z-e_y \right] _{k\times 1}\cdot x_{n\times 1} \\ &=x\cdot \left[ z-e_y \right] \end{align*} $$
其中，$z=\text{softmax}(\theta^Tx)$。注意，倒数第二步求出的结果是两个列向量相乘，不能运算。又已知结果应该是$n\times k$的矩阵，调整向量之间的顺序即可。

照猫画虎，可以写出batch的情况，$X\in R^{B\times n}$：

$$ \begin{align*} \frac{\partial}{\partial \theta}l_{ce}\left( \theta ^TX,y \right) &=\frac{\partial l_{ce}\left( \theta ^TX,y \right)}{\partial \theta ^TX}\cdot \frac{\partial \theta ^TX}{\partial \theta} \\ &=\left[ Z-E_y \right] _{B\times k}\cdot X_{B\times n} \\ &=X^T\cdot \left[ Z-E_y \right] \end{align*} $$

Lecture 3: Manual Neural Networks

这节课，我们将人工实现全连接神经网络，之后的课程，将引入自动微分技术。

从线性模型转变为非线性模型

image.png

如上图所示，线性模型本质上是将样本空间划分为线性的几个部分，这样的模型性能十分有限，因此很多不满足这样分布的实际问题就不能被解决。

一种解决方案是，在将样本输入到线性分类器前，先人工挑选出某些特征，即对$X$应用一个函数$\phi$，其将$X$映射到$\phi(X)$上，映射后的空间可以被线性划分。一方面，它确实是早期实践中行之有效的方案；另一方面，人工提取特征的泛化性能有限，受限于具体问题和研究人员的对问题的洞察程度。

如果我们使用线性网络提取特征，并直接接上一个线性分类头，这两个线性层等效为一个线性层，并不能做到非线性化的要求（基础知识，此处不再解释）。

因此，在使用线性网络提取特征后，需要再接上一个非线性函数$\sigma$，即$\phi = \sigma (W^T X)$。

神经网络

上文提到的使用非线性函数后的模型，就可以视作一种最简单的神经网络。所谓神经网络，值得是机器学习中某一类特定的假说模型，其由多层组成，每一层都有大量可以微分的参数。

神经网络最初的确起源于模拟人类神经元这一动机，但随着其发展，越来越多的神经网络模型出现，与人类大脑神经网络越来越不相关。

以双层神经网络为例，其形式化表示为$h_\theta(x) = W_2^T \sigma(W_1^T x)$，所有可学习的参数使用$\theta$表示。以batch的矩阵形式表示为：

$$ h_\theta(X) = \sigma(XW_1)W_2 $$
接下来给出L层多层感知机（a.k.a. MLP、前馈神经网络、全连接层）的形式化表达：
$$ \left\{\begin{array}{l} Z_{i+1} = \sigma_i(Z_iW_i), i=1,...,L \\ Z_1 = X\\ h_\theta(X) =Z_{L+1}\\ [Z_i\in R^{m\times n_i}, W_i \in R^{n_i\times n_{i+1}}]\\ \sigma_i:R\rightarrow R \end{array} \right. $$
每一层的输入为$Z_i$，输出为$Z_{i+1}$。

为什么要是用深度网络而不是宽度网络？没有很完美的解释，但最好并且最现实的解释是：经验证明，当参数量固定时，深度网络性能优于宽度网络。

反向传播（梯度计算）

与Lecture 2一致，使用交叉熵作为损失函数，使用SGD作为优化算法，唯一的区别是，这次要对MLP网络求解梯度。

对于两层神经网络$h_\theta(X) = \sigma(XW_1)W_2$，待求的梯度表达式为：

$$ \nabla_{\{W_1, W_2\}}l_{ce}(\sigma(XW_1)W_2,y) $$
对于$W_2$的梯度，其与Lecture 2的计算类似：
$$ \begin{align*} \frac{\partial l_{ce}(\sigma(XW_1)W_2,y)}{\partial W_2}&=\frac{\partial l_{ce}(\sigma(XW_1)W_2,y)}{\partial \sigma(XW_1)W_2} \cdot \frac{\partial\sigma(XW_1)W_2}{\partial W_2}\\ &=(S-I_y)_{m\times k}\cdot \sigma(XW_1)_{m\times d}\\ &=\sigma(XW_1)^T\cdot (S-I_y)\\ &[S=\text{softmax}(\sigma(XW_1))] \end{align*} $$

对于$W_1$的梯度，其需要多次应用链式法则，但并不难计算：

$$ \begin{align*} \frac{\partial l_{ce}(\sigma(XW_1)W_2,y)}{\partial W_1}&=\frac{\partial l_{ce}(\sigma(XW_1)W_2,y)}{\partial \sigma(XW_1)W_2} \cdot \frac{\partial\sigma(XW_1)W_2}{\partial \sigma(XW_1)}\cdot \frac{\partial \sigma(XW_1)}{\partial XW_1}\cdot\frac{\partial XW_1}{\partial X_1}\\ &=(S-I_y)_{m\times k}\cdot [W_2]_{d\times k}\cdot \sigma\prime(XW_1)_{m\times d}\cdot X_{m\times n}\\ &=X^T\cdot [\sigma\prime(XW_1)\odot((S-I_y)\cdot W_2^T)]\\ &[S=\text{softmax}(\sigma(XW_1))] \end{align*} $$
以上公式中$\odot$表示逐元素乘法。至于为啥这么算，俺也不知道。

接下来将其推广到一般情况，即$L$层的MLP中对$W_i$求导：

$$ \begin{align*} \frac{\partial l(Z_{l+1},y)}{\partial W_i} &=\frac{\partial l}{\partial Z_{l+1}}\cdot \frac{\partial Z_{l+1}}{\partial Z_{l}}\cdot...\cdot \frac{\partial Z_{i+2}}{\partial Z_{i+1}}\cdot\frac{\partial Z_{i+1}}{\partial W_{i}}\\ &=G_{i+1}\cdot\frac{\partial Z_{i+1}}{\partial W_{i}}=\frac{\partial l}{\partial Z_{i+1}}\cdot \frac{\partial Z_{i+1}}{W_i}\\ \end{align*} $$

由上述公式，我们可以得到一个反向迭代计算的$G_i$，即：

$$ \begin{align*} G_i &= G_{i+1}\cdot \frac{Z_{i+1}}{Z_i} \\ &=G_{i+1}\cdot \frac{\partial \sigma(Z_iW_i)}{\partial Z_iW_i}\cdot\frac{\partial Z_iW_i}{Z_i}\\ &=G_{i+1}\cdot \sigma\prime(Z_iW_i)\cdot W_i\\ \end{align*} $$

上面的计算都是将矩阵当作标量进行的，接下来我们考虑其维度。已知，$Z_i \in R^{m\times n_i}$是第$i$层的输入，$G_i = \frac{\partial l}{\partial Z_{i}}$，其维度如何呢？$G_i$每个元素表示损失函数$l$对第$i$层输入的每一项求偏导，也可以记作是$l$对$Z_i$求梯度，即$\nabla_{Z_i} l$，其维度显然是$m\times n_i$，继续计算前文$G_i$：

$$ \begin{align*} G_i &=[G_{i+1}]_{m\times n_{i+1}}\cdot \sigma\prime(Z_iW_i)_{m\times n_{i+1}}\cdot [W_i]_{n_i\times n_{i+1}}\\ &= [G_{i+1}\odot \sigma\prime(Z_iW_i)]W_i^T \end{align*} $$

有了$G_i$，就可以继续计算$l$对$W_i$的偏导数了：

$$ \begin{align*} \frac{\partial l(Z_{l+1},y)}{\partial W_i} &=G_{i+1}\cdot\frac{\partial Z_{i+1}}{\partial W_{i}} \\ &=G_{i+1}\cdot \frac{\partial\sigma(Z_iW_i)}{\partial Z_iW_i}\cdot\frac{\partial Z_iW_i}{\partial W_i}\\ &=[G_{i+1}]_{m\times n_{i+1}}\cdot \sigma\prime(Z_iW_i)_{m\times n_{i+1}}\cdot [Z_i]_{m\times n_i}\\ &=Z_i^T\cdot[G_{i+1}\odot\sigma\prime(Z_iW_i)] \end{align*} $$

至此，每个小组件都已制造完毕，让我们来把它装起来吧！

  • 前向传播
    • 初始化：$Z_1 = X$
    • 迭代：$Z_{i+1} = \sigma(Z_iW_i)$ 直至$i=L$（注意，最后一层没有非线性部分，此处没有展示出来）
  • 反向传播
    • 初始化：$G_{L+1} = S-I_y$
    • 迭代：$G_i=[G_{i+1}\odot \sigma\prime(Z_iW_i)]W_i^T$ 直至$i=1$ 值得注意的是，在反向传播中，需要用到前向传播的中间结果$Z_i$。为了更高效地计算梯度，不得不以牺牲内存空间为代价，即空间换时间。

许多课程，讲到这里就结束了，但对我们这门课来说，才刚刚开始…

Lecture 4: Automatic Differentiation

基本工具

  • 计算图 计算图是自动微分中常用的一种工具。计算图是一张有向无环图，每个节点表示（中间结果）值，每条边表示输入输出变量。例如，$y=f(x_1, x_2) = \ln(x_1)+x_1x_2-\sin x_2$对应的计算图为： 按照拓扑序列遍历这张图，就可以得到对应表达式的值。

对自动微分方法的简单介绍

深度学习中，一个核心内容就是计算梯度。这里介绍集中计算梯度的方案：

  • 偏导数定义

梯度是由一个个偏导数组成的，可以直接根据偏导数的定义来计算梯度：

$$ \frac{\partial f(\theta)}{\partial \theta_i} = \lim_{\epsilon \to 0}\frac{f(\theta + \epsilon e_i) - f(\theta)}{\epsilon} $$
其中，$e_i$是表示第$i$个方向上的单位向量。

  • 数值求解 根据上述定义，我们可以选取一个很小的量代入$\epsilon$，得到数值计算偏导的方法：
    $$ \frac{\partial f(\theta)}{\partial \theta_i} = \frac{f(\theta + \epsilon e_i) - f(\theta - \epsilon e_i)}{2\epsilon} + o(\epsilon^2) $$
    这里并不是直接使用第一项的公式，即分子不是$f(\theta + \epsilon e_i) - f(\theta)$，并且误差项是$\epsilon^2$，这是由于泰勒展开：
    $$ \begin{align*} f(\theta+\delta) = f(\theta)+f^\prime (\theta)\delta+\frac{1}{2}f^{\prime \prime}(\theta)\delta^2+o(\delta^3)\\ f(\theta-\delta) = f(\theta)+f^\prime (\theta)\delta-\frac{1}{2}f^{\prime \prime}(\theta)\delta^2+o(\delta^3) \end{align*} $$
    上述两式作差，即可得到数值计算$f^\prime(\theta)$的方法。

这个方法的问题在于存在误差，并且效率低下（这里要计算两次f），该方法常用于验证其它方法的具体实现是否出错。具体来说，验证如下等式是否成立：

$$ \delta^T \nabla_\theta f(\theta) = \frac{f(\theta + \epsilon \delta) - f(\theta - \epsilon \delta)}{2 \epsilon} + o(\epsilon^2) $$
其中$\delta$是单位球上的某个向量，$\nabla_\theta f(\theta)$是使用其它方法计算得到的梯度。等式左边是其它方法计算的梯度在$\delta$上的投影，右侧是使用数值求解得到的梯度值，验证该等式是否成立就可以判断左侧梯度是否计算错误。

  • 符号微分 符号微分，就是根据微分的计算规则使用符号手动计算微分。部分规则为：

    $$ \begin{align*} &\frac{\partial (f(\theta) + g(\theta))}{\partial \theta} = \frac{\partial f(\theta)}{\partial \theta} + \frac{\partial g(\theta)}{\partial \theta}\\ &\frac{\partial (f(\theta) g(\theta))}{\partial \theta} = g(\theta) \frac{\partial f(\theta)}{\partial \theta} + f(\theta) \frac{\partial g(\theta)}{\partial \theta}\\ &\frac{\partial f(g(\theta))}{\partial\theta}=\frac{\partial f(g(\theta))}{\partial g(\theta)}\frac{\partial g(\theta)}{\partial\theta} \end{align*} $$
    根据该公式，可以计算得到$f(\theta) = \prod_{i=1}^{n} \theta_i$的梯度表达式为：$\frac{\partial f(\theta)}{\partial \theta_k} = \prod_{j \neq k}^{n} \theta_j$。如果我们根据该公式来计算梯度，会发现需要计算$n(n-2)$次乘法才能得到结果。这是因为在符号运算的过程中，我们忽略了可以反复利用的中间结果。

  • 正向模式自动微分 forward mode automatic differentiation 沿着计算图的拓扑序列，同样可以计算出输出关于输入的导数，还是以$y=f(x_1, x_2) = \ln(x_1)+x_1x_2-\sin x_2$为例，其计算图为： image.png

整个梯度计算过程如下，在此过程中应用到了具体函数的求导公式：

$$ \begin{align*} &x_1 = 2\\ &x_2 = 5\\ &\dot v_{1} =1 \\ &\dot v_{2} =0 \\ &\dot{v}_{3} =\dot v_{1}/v_{1}=0.5 \\ &\dot{v}_{4} =\dot{v}_{1}v_{2}+\dot v_{2}v_{1}=1\times5+0\times2=5 \\ &\dot v{5} =\dot{v_{2}}\cos v_{2}=0\times\cos5=0 \\ &\dot{v}_{6} =\dot v_{3}+\dot v_{4}=0.5+5=5.5 \\ &\dot{v}_{7} =\dot{v_{6}}-\dot{v_{5}}=5.5-0=5.5 \end{align*} $$

对于$f:\mathbb{R}^n \to \mathbb{R}^k$，前向传播需要$n$次前向计算才能得到关于每个输入的梯度，这就意味前向传播适合$n$比较小、$k$比较大的情况。但是在深度学习中，通常$n$比较大、$k$比较小。

  • 反向模式自动微分 定义$\text{adjoint}:\overline{v_i}=\frac{\partial y}{\partial v_i}$,其表示损失函数对于参数$v_i$的偏导。 整个计算过程如下所示，需要注意的是$\overline{v_2}$的计算过程，其在计算图上延伸出了两个节点，因此梯度也由两部分相加：
    $$ \begin{align*} &\overline{v_{7}}=\frac{\partial y}{\partial v_{7}}=1\\ &\overline{v_{6}}=\overline{v_{7}}\frac{\partial v_{7}}{\partial v_{6}}=\overline{v_{7}}\times1=1\\ &\overline{v_{5}}=\overline{v_{7}}\frac{\partial v_{7}}{\partial v_{5}}=\overline{v_{7}}\times(-1)=-1\\ &\overline{v_{4}}=\overline{v_{6}}\frac{\partial v_{6}}{\partial v_{4}}=\overline{v_{6}}\times1=1\\ &\overline{v_{3}}=\overline{v_{6}}\frac{\partial v_{6}}{\partial v_{3}}=\overline{v_{6}}\times1=1\\ &\overline{v_{2}}=\overline{v_{5}}\frac{\partial v_{5}}{\partial v_{2}}+\overline{v_{4}}\frac{\partial v_{4}}{\partial v_{2}}=\overline{v_{5}}\times\cos v_{2}+\overline{v_{4}}\times v_{1}\\ &\overline{v_{1}}=\overline{v_{4}} \frac{\partial v_{4}}{\partial v_{1}}+\overline{v_{3}} \frac{\partial v_{3}}{\partial v_{1}}=\overline{v_{4}}\times v_{2}+ \overline{v_{3}} \frac{1}{v_{1}}=5+\frac{1}{2}=5.5 \end{align*} $$

接下来我们讨论一下为什么前文中$\overline{v_2}$由两部分组成。考虑如下一个计算图： image.png

$y$可以被视作关于$v_2$和$v_3$的函数，即$y = f(v_2, v_3)$，那么：

$$ \overline{v_{1}}=\frac{\partial y}{\partial v_{1}}=\frac{\partial f(v_{2},v_{3})}{\partial v_{2}}\frac{\partial v_{2}}{\partial v_{1}}+\frac{\partial f(v_{2},v_{3})}{\partial v_{3}} \frac{\partial v_{3}}{\partial v_{1}}=\overline{v_{2}} \frac{\partial v_{2}}{\partial v_{1}}+\overline{v_{3}} \frac{\partial v_{3}}{\partial v_{1}} $$
因此，定义partial adjoint $\overline{v_{i\to j}} = \overline{v_j} \frac{\partial v_j}{\partial v_i}$，那么$\overline{v_i}$可以表示为：
$$ \overline{\nu_i}=\sum_{j\in next(i)}\overline{\nu_{i\rightarrow j}} $$

反向模式微分算法的实现

基于以上分析，可以写出如下的实现反向模式微分算法的伪代码： image.png

其中node_to_grad是一个字典，保存着每个节点的partial adjoint值。由于是按照逆拓扑序列遍历的节点，因此可以保证当遍历到$i$时，所有以$i$为输入的节点（k节点所在的集合）都已被遍历完毕，即$\overline{v_k}$已经计算出来。

那么partial adjoint值使用什么数据结构保存呢？一个常见的思路是使用邻接矩阵，但是这个矩阵中有大量元素是不存在了，空间浪费很大。我们可以在原有计算图的基础上进行拓展来保存partial adjoint和adjonitzhi之间的计算关系。

如下图所示，黑色部分是原表达式的计算图，红色部分是将adjoint和partial adjount的计算图： image.png

使用计算图，除了能够节省内存外，还能清楚的看到正向计算的中间结果和反向计算之间的依赖关系，进而优化计算。

反向模式ad和反向传播的区别

image.png

反向传播：

  • 在反向计算过程中使用与前向传播完全相同的计算图
  • 应用于第一代深度学习框架

反向AD：

  • 为adjoint在计算图中创建独立的节点
  • 被应用于现代深度学习框架

现代普遍应用反向AD的原因：

  • 某些损失函数是关于梯度的函数，这种情况下需要计算梯度的梯度，但反向传播就不能计算此类情况，而在反向AD中只要增加一个节点后在此计算梯度即可；
  • 反向AD优化空间更大。

考虑Tensor的反向模式AD

前面都是在假设中间变量是标量的基础上讨论的，接下来我们将其推广到Tensor上。

首先推广adjoint，定义对于一个Tensor$Z$，其adjoint$\overline{Z}$为：

$$ =\begin{bmatrix}\frac{\partial y}{\partial Z_{1,1}}&...&\frac{\partial y}{\partial Z_{1,n}}\\...&...&...\\\frac{\partial y}{\partial Z_{m,1}}&...&\frac{\partial y}{\partial Z_{m,n}}\end{bmatrix} $$
鉴于
$$ \begin{align*}Z_{ij}&=\sum_kX_{ik}W_{kj}\\v&=f(Z)\end{align*} $$
那么在计算$\overline{X_{i,k}}$时，需要将所有计算图上以$X_{i,k}$为输入的节点都找出来，即$Z$的第$i$行的每个元素。因此$\overline{X_{i,k}}$的计算公式为：
$$ \overline{X_{i,k}}=\sum_{j}\frac{\partial Z_{i,j}}{\partial X_{i,k}}\bar{Z}_{i,j}=\sum_{j}W_{k,j}\bar{Z}_{i,j} $$
上述公式记为矩阵形式为：
$$ \overline X = \overline Z W^T $$

Lecture 5: Automatic Differentiation Implementation

这讲主要介绍我们hw中要实现的needle的总体框架，项目中已给出了约1000行代码。

autograd.py

autograd保存与实现自动微分相关的代码。

Value类对应计算图上的节点，其数据成员包括：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Value:
    """A value in the computational graph."""

    # trace of computational graph
    op: Optional[Op]
    inputs: List["Value"]
    # The following fields are cached fields for
    # dynamic computation
    cached_data: NDArray
    requires_grad: bool

op用于保存该节点的运算符，inputs保存该运算符的操作数，cached_data保存该节点的数值，其数据结构因平台不同而区别。

ops

本节主要介绍needle库的代码结构，笔记相当草率，建议看原视频。

ops文件夹（2023版本）或者op.py（2022）版本保存各种算子的实现。 Op类规定了两个必须要实现的接口：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class Op:
    """Operator definition."""

    def compute(self, *args: Tuple[NDArray]):
        """Calculate forward pass of operator.

        Parameters
        ----------
        input: np.ndarray
            A list of input arrays to the function

        Returns
        -------
        output: nd.array
            Array output of the operation

        """
        raise NotImplementedError()

    def gradient(
        self, out_grad: "Value", node: "Value"
    ) -> Union["Value", Tuple["Value"]]:
        """Compute partial adjoint for each input value for a given output adjoint.

        Parameters
        ----------
        out_grad: Value
            The adjoint wrt to the output value.

        node: Value
            The value node of forward evaluation.

        Returns
        -------
        input_grads: Value or Tuple[Value]
            A list containing partial gradient adjoints to be propagated to
            each of the input node.
        """
        raise NotImplementedError()

compute接口用于描述该运算符实施的运算，gradient描述该运算符对应的梯度计算方式。

Lecture 6: Fully connected network, optimization, initialization

全连接网络

之前我们讨论的全连接网络都是不含偏执项的（为了方便进行手动微分），本章将介绍真正的MLP。其通过迭代的过程进行定义：

$$ \begin{align*} &z_{i+1} = \sigma_i(W_i^Tz_i+b_i), \ \ \ i=1,...,L\\ &h_\theta(x) = z_{L+1}\\ &z_1 = x \end{align*} $$
上述模型中，可优化的参数集合为$\theta = {W_{1:L}, b_{1:L} }$。$\sigma_i(x)$是非线性的激活函数，特别的，最后一层没有激活函数，即$\sigma_L (x)= x$。

迭代的表达式写成矩阵形式为：

$$ \begin{align*} Z_{i+1} = \sigma_i(Z_iW_i+1b_i^T) \end{align*} $$
其中，$1$表示一个表示一个全1的列向量，用于将列向量$b_i^T$广播到与矩阵$Z_iW_i$相匹配的形状。

在实际实现过程中，我们不用浪费空间去构造这样一个全1列向量，而是直接使用广播算子。在NumPy有许多自动的广播操作，但是在我们实现的needle库中，这一操作更加显式，例如对于$(n\times 1) \to (m \times n)$，要执行的操作为A.reshape((1, n)).broadcast_to((m, n))。

优化

对于有监督的深度学习任务，一般的优化目标为：

$$ \mathop{\text{minimize}}_{\theta} \ \ f(\theta) = \frac{1}{m}\sum_{i=1}^m{l(h_\theta(x^{(i)},y^{(i)}))} $$
接下来将介绍几常用的优化算法。

  • 梯度下降 gradient desecent 梯度下降法之前几节课讲过了，这里直接给出其数学表达式：
    $$ \theta_{t+1} = \theta_t - \alpha \nabla_\theta f(\theta_t) $$
    其中，$t$表示迭代次数。

学习率这一参数对于该方法格外重要，不同的学习率的表现相差很大很大： image.png

上图展示了大学习率和小学习率的迭代过程，如果目标函数再复杂一点，那么确定合适的学习率就会变得更加复杂。接下来将介绍一些不同的方法，它们各有其收敛行为。

对于梯度下降法的改进，有两种方案：梯度计算的变种和随机的变种。首先介绍第一类。

  • 牛顿法 Newton’s Method 牛顿发使用二次曲面对一个高维函数做近似，因此其收敛速度显著快于一阶逼近的梯度下降法。其迭代公式为：
    $$ \theta_{t+1} = \theta_t - \alpha(\nabla_\theta^2f(\theta_t))^{-1}\nabla_\theta f(\theta_t) $$
    其中，$(\nabla_\theta^2f(\theta_t))^{-1}$是Hessian矩阵的逆矩阵。Hessian矩阵每个元素都是二阶导数，其具体定义为：
    $$ \nabla_\theta^2f(\theta_t) = H=\begin{bmatrix}\frac{\partial^2f}{\partial x_1^2}&\frac{\partial^2f}{\partial x_1\partial x_2}&\cdots&\frac{\partial^2f}{\partial x_1\partial x_n}\\\frac{\partial^2f}{\partial x_2\partial x_1}&\frac{\partial^2f}{\partial x_2^2}&\cdots&\frac{\partial^2f}{\partial x_2\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\frac{\partial^2f}{\partial x_n\partial x_1}&\frac{\partial^2f}{\partial x_n\partial x_2}&\cdots&\frac{\partial^2f}{\partial x_n^2}\end{bmatrix} $$
    对于二次函数，牛顿法可以一次给出指向最优点的方向

这一方法广泛用于传统凸优化领域，但是很少用于深度学习优化。有两个主要原因：1) Hessian矩阵是$n\times n$的，因此参数量稍微大一点其计算代码都非常非常恐怖；2) 对于非凸优化，二阶方法是否更有效还有待商榷。

  • 动量梯度下降法 Momentum 在普通梯度下降法中，如果学习率太大，就会出现来回横跳的情况，如果对前几次梯度取平均，则可能改善这一情况。

动量法正是对梯度取指数移动平均1的方案，具体来说有：

$$ \begin{align*} &u_{t+1} = \beta u_t +(1-\beta)\nabla_\theta f(\theta_t)\\ &\theta_{t+1} = \theta_t - \alpha u_{t+1} \end{align*} $$
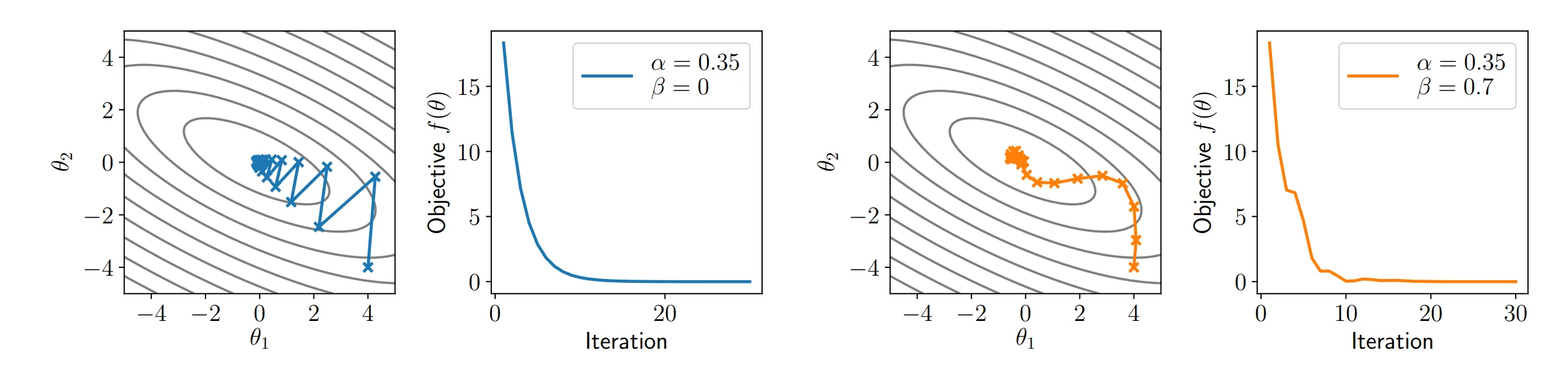
该方法可视化过程如下图所示，在较大学习率的情况下，其相比梯度下降法优化曲线更为平滑。 image.png

  • 无偏动量法 Unbiasing momentum 前一章节实际上有一个小瑕疵。如果$u_0$初始化为0，那么第一次进行更新是的梯度值是正常更新的$(1-\beta)$倍，因此其前期的收敛过程会稍慢，随着迭代的进行，其效应会逐渐减弱。

为了修正其影响，我们可以在参数更新过程中对动量进行缩放，具体来说：

$$ \theta_{t+1} = \theta_{t} - \frac{\alpha u_{t+1}}{1-\beta^{t+1}} $$
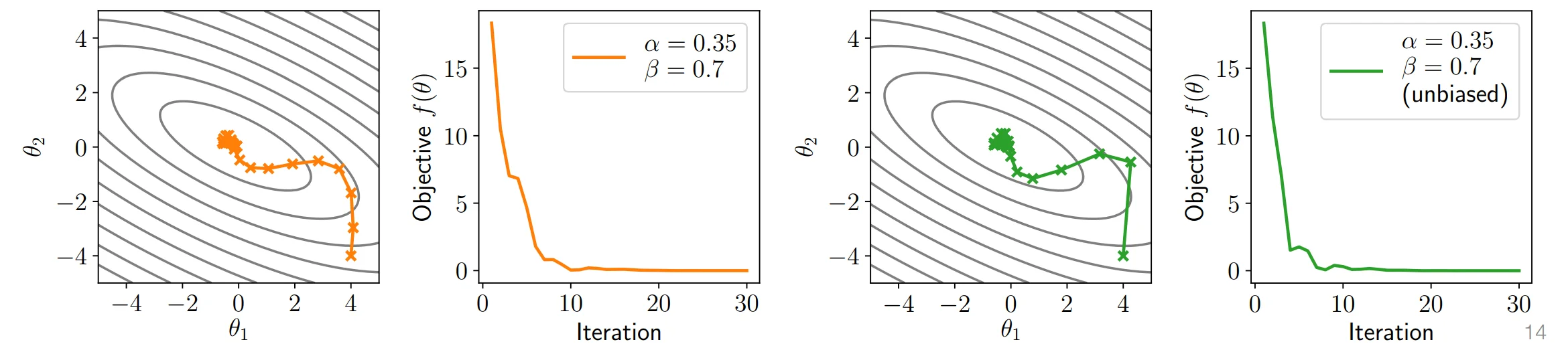
如下图所示，修正以后其前期的更新速度要快了不少。 image.png

  • Nesterov momentum Nesterov是梯度下降中一个非常有效的“trick”，其在传统momentum的基础上，将计算当前位置的梯度改为计算下一步位置的梯度。即：
    $$ u_{t+1} = \beta u_t +(1-\beta)\nabla_\theta f(\theta_t - \alpha u_t) $$
    关于其为啥有效，看到了两篇文章。第一篇2通过推导认为该方案对二阶导数进行了近似，因此其收敛速度更快；第二篇3认为其能够更好地感知未来位置的梯度，在未来梯度很大时放慢步子。

不看广告看疗效，对比普通Momentum，该方法的收敛速度要快得多。据说其也更适合一个深度网络。 image.png

  • Adam Adam是一种自适应的梯度下降算法。不同参数其对应的梯度之间的大小差异可能很大，Adam对此的解决方案是提供一个缩放因子，梯度值小则将其缩放得大一点，即：
    $$ \begin{align*} &u_{t+1} = \beta_1 u_t + (1-\beta_1)\nabla_\theta f(\theta_t)\\ &v_{t+1} = \beta_2 v_t + (1-\beta_2)(\nabla_\theta f(\theta_t))^2 &\text{平方为逐元素运算}\\ &\theta_{t+1} = \theta_t - \frac{\alpha u_{t+1}}{\sqrt{v_{t+1}}+\epsilon} & \text{所有元素均为逐元素运算}\\ \end{align*} $$
    Adam在实践中得到了广泛应用，在特定任务上，其可能不是最佳的优化器（如下图），但在大部分任务上，其都能有不错的可以作为基线的表现。 image.png

接下来将介绍随机变种。随机变种是在优化过程中加入了随机变量（噪声），例如每次使用数据集的一个子集对参数进行更新。

  • 随机梯度下降 Stochastic gradient descent 随机梯度下降正是每次使用数据集的一个子集对参数进行更新，即：
    $$ \theta_{t+1} = \theta_t - \frac{\alpha}{|B|}\sum_{i\in B}\nabla_\theta l(h_\theta(x^{(i)},y^{i})) $$

看上去SGD的迭代次数比梯度下降要多得多，但是其每轮迭代的计算代价都要小的多，同时 image.png

尽管在凸优化上可视化训练过程给了很直观的感受，但需要注意的是，深度学习并不是凸优化或者二次函数，这些优化方法在深度学习上的应用与在凸优化上的效果可能完全不同。

初始化

参数的初始值如何确定？这是个好问题。

在凸优化中，尝尝将所有参数初始化为0，如果在神经网络中也这么做，那么每一层的输出都是0，求得的梯度也都是0🙁。全0是这个模型的一个不动点，模型将永远得不到更新。

  • 初始化参数对梯度的影响很大 一种自然的想法是对参数进行随机初始化，例如按照多元正态分布进行初始化。但是，分布中参数的选择对于梯度的影响可能会相当大，如下图所示： image.png 随着层数的增加，如果激活值范数变化的太剧烈，会导致梯度爆炸或者消失问题，如果梯度值过大或者过小，也会导致这些问题。

  • 权重的在训练过程的变化可能很小 可能存在这样一个误区：无论初始值如何选择，这些参数最终都会收敛到某个区域附近。事实并非如此，整个训练过程中权重的变化并非如此剧烈。

  • 为什么2/n在前面是个合适的初始化参数 这里直接使用gpt对这页ppt的解释

考虑独立的随机变量 𝑥∼𝑁(0,1)x∼N(0,1) 和 𝑤∼𝑁(0,1𝑛)w∼N(0,n1​)，其中 𝑥x 是输入，𝑤w 是权重。

期望和方差

  • 𝐸[𝑥⋅𝑤𝑖]=0E[x⋅wi​]=0
  • Var[𝑥⋅𝑤𝑖]=1𝑛Var[x⋅wi​]=n1​

因此，对于 𝑤𝑇𝑥wTx：

  • 𝐸[𝑤𝑇𝑥]=0E[wTx]=0
  • Var[𝑤𝑇𝑥]=1Var[wTx]=1（根据中心极限定理，𝑤𝑇𝑥wTx 服从 𝑁(0,1)N(0,1)）

激活值的方差

如果使用线性激活函数，并且 𝑧𝑖∼𝑁(0,𝐼)zi​∼N(0,I)，则 𝑊𝑖∼𝑁(0,1𝑛𝐼)Wi​∼N(0,n1​I)，那么：

𝑧𝑖+1=𝑊𝑖𝑧𝑖zi+1​=Wi​zi​

ReLU 非线性

如果使用 ReLU 非线性激活函数，由于 ReLU 会将一半的 𝑧𝑖zi​ 分量设为零，因此为了达到相同的最终方差，需要将 𝑊𝑖Wi​ 的方差增加一倍。因此：

𝑊𝑖∼𝑁(0,2𝑛𝐼)Wi​∼N(0,n2​I)

这就是所谓的 Kaiming 正态初始化（He 初始化），它特别适用于 ReLU 激活函数。

Lecture 7: Neural Network Library Abstractions

这节课主要介绍如何使用我们的needle库来实现一些简单的深度学习模型，构造一些小组件。

程序抽象

现代成熟的深度学习库提供了一些API，站在今天的视角，这些API都是都是恰到好处的。通过思考为什么要这样设计接口，可以让我们更好地理解深度学习库在进行程序抽象时的内部逻辑。

首先几个经典的深度学习框架进行分析，包括Caffe、TensorFlow和PyTorch。

  • Caffe 1.0 （2014） 在Caffe中，使用Layer这一概念来表示神经网络中的一个个小模块，通过拼接和替换Layer，可以实现快速构造和修改神经网络，并使用同一套代码进行训练。

Layer类提供了forward和backward两个接口：

1
2
3
4
5
6

class Layer:
	def forward(bottom, top):
		pass

	def backward(top, propagate_down, bottom):
		pass

forward负责将来自bottom的数据进行前向传播，然后将数据保存到top中。在backward接口中，top保存来自输出的梯度，propagate_down用以指示是否要对其求梯度，bottom用于存放梯度。

在Caffe中，计算梯度是“就地”完成的，而非在计算图上新增额外的节点。作为第一代深度学习框架，直接计算梯度的思想是朴素但是符合直觉的。

  • TensorFlow 1.0 （2015） 作为第二代深度学习框架，其在引入了计算图的概念。在计算图中，只要定义前向计算的计算方式，当需要计算梯度时，直接对计算图进行拓展即可。一个简短实例为：
1
2
3
4
5
6
7
8
9

import tensorflow as tf

v1 = tf.Variable()
v2 = tf.exp(v1)
v3 = v2 + 1
v4 = v2 * v3

sess = tf.Session()
value4 = sess.run(v4, feed_dict = {v1: numpy.array([1])})

以上代码v1~4仅仅是占位符，用于构建计算图，在没有输入传入前并没有值。通过会话来获取某个输入的情况下输出的值。

上述过程被称为声明式编程。即计算图在定义时并不会立即执行，而是等到会话（session）运行时才执行。这种方式的优点有：代码分区，可读性高；运行前计算图已知，可以针对性优化；通过会话便于实现分布式计算

  • PyTorch (needle) PyTorch使用的是命令式编程，相比声明式编程，命令式编程在构建计算图时就已经指定其值。
1
2
3
4
5
6

import needle as ndl

v1 = ndl.Tensor([1])
v2 = ndl.exp(v1)
v3 = v2 + 1
v4 = v2 * v3

命令式编程可以很方便地与Python原生控制流语句结合在一起，例如：

1
2
3
4

if v4.numpy() > 0.5:
	v5 = v4 * 2
else:
	v5 = v4

tf1.0的效率更高，适合推理和部署。PyTorch1.0则更适合开发和debug。

高级模块化库组件

如何使用深度学习库来实现深度学习呢？在hw1中我们使用一个个底层算子来搭建模型和实现训练过程，但这样开发太低效了。深度学习本身是很模块化的：由模型、损失函数和优化方法三部分组成。不但如此，模型本身也是高度模块化的。因此，我们在实现深度学习库时，必须精心设计好接口，以便支持该模块化的特性。

在PyTorch中，有一类叫做nn.Module，对应的就是模型中一个个小的子模块，其特点是以Tensor同时作为输入和输出。损失函数也满足这一特性，其可以被视为一个模块。

对于优化器，其作用是输入一个模型，对该模型中的参数按照某一规则进行更新。

为了防止过拟合，有些模型还具有正则项，其有两种实现方式：

  • 作为损失函数的一部分进行实现
  • 直接整合进优化器中

参数初始化同样很重要，其一般在构建nn.Module中指定。

数据加载也是一个很重要的模块。数据加载中还经常对数据进行预处理和增强。

各组件之间数据流图如下所示： image.png

Lecture 8: Neural Network Implementation

修改Tensor的data域

在实现SGD时，由于存在多个batch，可能会在一个循环里对待学习参数进行更新，即：

1
2

for _ in range(iterations):
	w -= lr * grad

正如在CMU 10-414 Assignments 实验笔记 > SGD for a two-layer neural network踩过的坑那样，直接使用Tensor之间的算子进行参数更新会导致每次更新都会在计算图上增加一个新的节点w，这个节点具有Op和inputs，严重拖累反向传播速度。

为了避免每次更新参数时都在计算图上留下一个需要求梯度的节点，needle库提供了Tensor.data()方法，用于创建一个与Tensor共享同一个底层data的节点，但其不存在Op和inputs，也不用对其进行求导。

因此，可以使用Tensor.data方法，在不干扰计算图反向传播的前提下对参数进行正常的更新，即：

1

w.data -= lr * grad.data

数值稳定性

每个数值在内存中的存储空间都是有限的，因此保存的数值的范围和精度都是有限的，计算过程中难免出现溢出或者精度丢失的情况，在实现算子时，必须考虑到数值稳定性的问题。

例如，在softmax公式中，由于指数运算的存在，数值很有可能就上溢了，一个修正方式是在进行softmax运算前，每个元素都减去输入的最大值，以防止上溢。即：

$$ z_i = \text{softmax}(x_i) = \frac{\exp(x_i -c)}{\sum_k {\exp(x_k-c)}} $$
其中，$c = \max(x)$。

类似的，其它算子也要考虑相应的稳定性问题。

Parameter 类

Parameter类用于表示可学习的参数，其是Tensor的子类。相比Tensor类，这个类不必再引入新的行为或者接口，因此其实现很简单：

1
2

class Parameter(ndl.Tensor):
    """parameter"""

Module 类

Module类用于表示神经网络中一个个子模块。其具有如下接口：

  • parameters：获取模块中所有可学习参数
  • __call__：进行前向传播 在实现时，定义了一个辅助函数_get_params用于提取一个模块中的所有可学习参数。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

def _get_params(value):
    if isinstance(value, Parameter):
        return [value]
    if isinstance(value, dict):
        params = []
        for k, v in value.items():
            params += _get_params(v)
        return params
    if isinstance(value, Module):
        return value.parameters()
    return []

class Module:
    def parameters(self):
        return _get_params(self.__dict__)

    def __call__(self, *args, **kwargs):
        return self.forward(*args, **kwargs)

Optimizer 类

Optimizer类用于优化模型中可学习参数，其有两个关键接口：

  • reset_grad：重置模型中可学习参数的grad字段
  • step：更新参数值 reset_grad实现比较简单，step方法则依赖于优化算法的具体实现：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Optimizer:
    def __init__(self, params):
        self.params = params

    def reset_grad(self):
        for p in self.params:
            p.grad = None

    def step(self):
        raise NotImplemented()

Lecture 9: Normalization and Regularization

Normalization

在前面几讲提到过，参数初始值的选择对于模型的训练很重要，不恰当的初始值参数会导致梯度消失或者爆炸💥。更重要的是，当训练完成后，这些梯度和参数值大小仍有初始值差不多，这更强调了初始值的重要性。 image.png

为了修复这一问题，引入了layer normalization。其思想就是对激活层的输出进行标准化，即将输出减去期望后除以标准差：

$$ \begin{align*} \hat{z}_{i+1} &= \sigma_i (W_i^Tz_i+b_i)\\ z_{i+1} &=\frac{\hat{z}_{i+1} - E(\hat{z}_{i+1})}{Var(\hat{z}_{i+1})+\epsilon} \end{align*} $$
上述技巧目前已经得到广泛应用，但在实践中，应用layer norm会导致模型难以收敛到一个很小的loss值。

另外一种技巧是batch norm。layer norm是对每一个sample（z的每一行）做归一化，而batch norm对每一列归一化。这一方法使得每个batch的所有样本都会对该batch中某个样本的推理结果有影响，因此在进行推理时，batch norm中的归一化的参数应该使用整个训练集上的参数，而非推理时输入样本的batch参数。

Regularization

正则化用于对抗过拟合，所谓过拟合是指模型在训练集上性能非常好，但在测试机上泛化性能很差。正则化就是限制参数复杂度的过程，可以分为显式正则和隐式正则。

隐式正则化是指现有算法或架构在不显式添加正则化项的情况下，自然地对函数类进行限制。具体来说，隐式正则化通过以下方式实现：

  • 算法的固有特性：例如，随机梯度下降（SGD）等优化算法在训练过程中自带某些正则化效果。虽然我们并没有显式地优化所有可能的神经网络，而是通过SGD优化那些在特定权重初始化下的神经网络。这种优化过程本身对模型的复杂度进行了限制。
  • 架构的设计：某些网络架构设计本身就具有正则化效果。例如，卷积神经网络（CNN）的共享权重机制和局部连接特性，自然地减少了模型参数的数量，从而降低了模型复杂度。

显式正则化指的是通过显式得修改模型使其能够避免对训练集过拟合。

一种最常见的应用于参数的正则化方案是l2正则化，即l2 regularization a.k.a weight decay。传统认为，模型参数值的大小可以在一定程度上指示出模型的复杂度，因此通过在优化目标中引入l2正则项来控制模型的大小。一般地，引入l2 regularization的机器学习优化问题可以表示为：

$$ \mathrm{minimize} \quad \frac{1}{m}\sum_i^m{l(h_{w_{1:L}}(x^{(i)}, y^{(i)}))}+\frac{\lambda}{2}\sum_{i=1}^L{||w_i||_F^2} $$
其中，$||w_i||_F$是Frobenius范数，其表示矩阵每个元素的平方和的平方根。

得益于这里的系数是$1/2$，在对$w_i$求导时正则项恰好为$\lambda w_i$。梯度更新的公式相应变为：

$$ W_i :=(1-\alpha \lambda)W_i-\alpha \nabla \frac{1}{m}l $$

注意，引入l2正则化后，每轮迭代都会将参数缩小至原来的$1-\alpha \lambda$。很多地方不将l2正则化作为损失函数的一部分，而是将其作为优化器的一部分，即直接将参数进行缩小，这种方法被称为weight decay，显然二者是等价的。

另外一种正则化方法是dropout，其思想是在训练过程中随机地将一些激活层的输出置为0，并对其它输出放大，以确保整层输出的数学期望不变，形式化表示为：

$$ \begin{align*} \hat{z}_{i+1} &= \sigma_i(W^T_i z_i)+b_i\\ (z_{i+1})_j &= \begin{cases} ((\hat{z}_{i+1} )_j)/(1-p) \quad &\text{以概率}1-p\\ 0 &\text{以概率}p \end{cases} \end{align*} $$
在推理时，则不需要进行dropout。

直观地说，dropout能够提升模型在激活层部分缺失时进行推理的能力，但显然这一能力没什么卵用。另一种解释是dropout提升了模型训练过程中的随机性，类似SGD。

Lecture 10: Convolutional Networks

Convolutional operators in deep networks

在hw2中，我们通过flatten操作将图片视作一个序列进行计算，这对于小尺寸的图片是可行的，但对于大尺寸的图片，例如256×256的图片，将会导致输入异常庞大，网络也随之变大。这种简单粗暴的处理方式不利于提取图片的内在特征，例如，如果对图片进行平移，其输入序列的变化相当大。

卷积网络出于以下两个动机：

  • 层之间的激活以局部的方式发生，并且隐藏层的输出也被视为图像
  • 在所有的空间位置共享权重

卷积网络有以下两个优点：

  • 使用的参数很少。参数量由卷积网络的大小决定，而和输入的shape无关；
  • 能够很好地捕获图片的内在不变形。

卷积的计算示意如下图所示，卷积核在原图上滑动，从而产生一张新的图片。 image.png

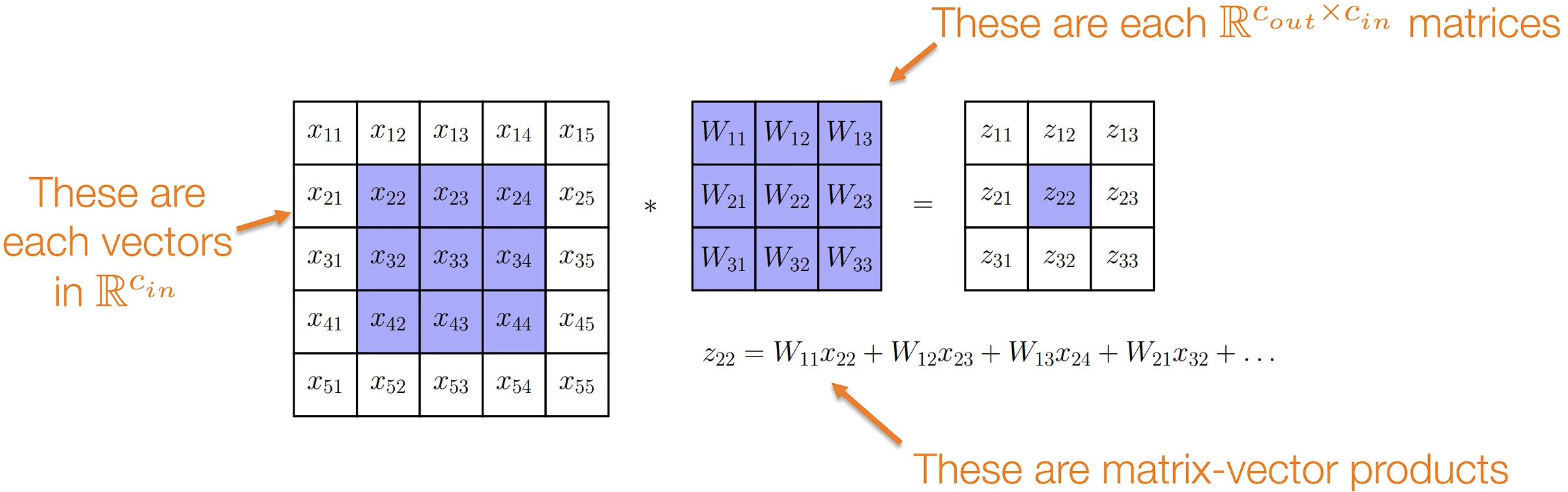
在深度学习中，输入和隐藏层都很少是一个1D的矩阵，一般而言，其是由多个通道的。例如，一张彩色图片由RGB三通道组成，而中间的隐藏层，通常会有比较大的通道数，如下图所示： image.png 记卷积层的输入$x\in \mathbb{R}^{h\times w \times c_{in}}$，输出$z\in \mathbb{R}^{h\times w \times c_{out}}$。从上图可以发现，卷积输出的某个通道，都是由输入在同一个局部的所有通道共同决定的，因此，卷积核$W\in \mathbb{R}^{c_{in}\times c_{out}\times k \times k}$，卷积过程可以形式化表示为：

$$ z[:,:,s] = \sum_{r=1}^{c_{in}}x[:,:,r] \cdot W[r,s,:,:] $$
关于多通道卷积，另外一种更符合直觉的理解是将相同位置的各通道的组合看作是一个向量，即下图中，$x$每一格都是一个向量，$W$每一格都是$c_{out} \times c_{in}$的矩阵，卷积的输出由对应位置的$z$和$W$按矩阵乘法并求和得到。 image.png

Elements of practical convolutions

在实际的卷积操作中，通常还会应用一些别的技术。

  • Padding 原始的卷积操作，会将输出的长宽变小$k-1$个长度，通过在周围填充$(k-1)/2$个0元可以保证输出的shape与输入一致。为了避免两侧填充不一致这个别扭的情况，我们一般选取卷积核大小为奇数。

  • Strided Convolutions / Pooling 经过padding之后的卷积操作，不改变图片的shape，但在实际应用中，通常会对图片进行下采样。用两种解决方案：

  1. 使用最大/平均池化来聚合信息，例如，使用一个2×2的核进行池化操作，每次移动的步长为2，就可以将整张图片长宽各放缩至原来一半；
  2. 卷积操作时，卷积核移动的步长大于1。

  • Grouped Convolutions 当输入和输出的通道数很大时，卷积核的参数量仍可能非常非常大。一种解决方案是，使用分组卷积，即将输入通道分为多个组，每个组独立进行卷积操作，如下图所示。如果分为G组，则参数量可减少为原来的1/G。 image.png

  • Dilations 传统卷积的感受野和卷积核一样大，扩张卷积的思路是在卷积区域中插入间隔，能够扩大卷积核的感受野。下图表示的很形象。 image.png

Differentiating convolutions

正如前文所提到的，我们可以通过一系列矩阵向量乘法和求和运算来实现卷积操作，但这么做效率太低了，我们的计算图上有很多中间节点，这些中间变量将消耗大量的内存空间。因此，我们不应该使用微分库中的算子来计算卷子，而是将其作为一个算子来实现，并手动计算其微分。

首先定义卷积操作：

$$ z = \operatorname{conv}(x,W) $$
$z$的梯度怎么与adjoints乘呢？这是个问题。$z$的梯度有以下二者：$\frac{\partial z}{\partial x}$和$\frac{\partial z}{\partial W}$，从形式上看，他们是3阶张量初以四阶张量，相当复杂。

首先考虑最简单的矩阵和向量相乘的情况，即：

$$ z = Wx $$
那么$z$对$x$的导数就是$W$，即其与adjoint的乘法计算公式为：
$$ W^T\bar{v} $$
也就是说如果在前向传播中我们计算一个矩阵和向量的乘积，那么在反向传播中，我们要计算这个矩阵的转置和adjoint的乘积。那对于卷积来说，它的“转置”是什么呢？

  • 将卷积视为矩阵运算I 以1d卷积为例，我们考虑如下的一个卷积运算，其中每个格子都是一个向量或者矩阵。 image.png 将上面这个矩阵运算展开，可以得到：
    $$ \begin{bmatrix}z_1\\z_2\\z_3\\z_4\\z_5\end{bmatrix}=x*w=\begin{bmatrix}w_2&w_3&0&0&0\\w_1&w_2&w_3&0&0\\0&w_1&w_2&w_3&0\\0&0&w_1&w_2&w_3\\0&0&0&w_1&w_2\end{bmatrix}\begin{bmatrix}x_1\\x_2\\x_3\\x_4\\x_5\end{bmatrix} $$
    有了$\hat{W}$，我们可以很容易地写出$\hat{W}^T$,即：
    $$ \hat W^T=\begin{bmatrix}w_2&w_1&0&0&0\\w_3&w_2&w_1&0&0\\0&w_3&w_2&w_1&0\\0&0&w_3&w_2&w_1\\0&0&0&w_3&w_2\end{bmatrix} $$
    不难发现，这个算子实际上是$[w_3, w_2, w_1]$这个卷积核，即原始卷积核翻转后的卷积核。也就是说，梯度和adjoint的乘积可以表示为：
    $$ \hat{v}\frac{\partial \operatorname{conv}(x,w)}{\partial x} = \operatorname{conv}(\hat{v},\operatorname{flip}(w)) $$
  • 将卷积视为矩阵运算II 接下来我们考虑卷积对于参数$w$的导数。同样，我们将矩阵运算展开，可以得到：
    $$ \begin{bmatrix}z_1\\z_2\\z_3\\z_4\\z_5\end{bmatrix}=x*w=\begin{bmatrix}0&x_1&x_2\\x_1&x_2&x_3\\x_2&x_3&x_4\\x_3&x_4&x_5\\x_4&x_5&0\end{bmatrix}\begin{bmatrix}w_1\\w_2\\w_3\end{bmatrix} $$
    相比矩阵运算I，我们构造出的$\hat{X}$矩阵是一个密集矩阵，在实现卷积算子时，我们常常采用这个方案来运算。这个$\hat{X}$矩阵被称为“im2col”矩阵（image to column）。

Lecture 11: Hardware acceleration

General acceleration techniques

现代机器学习框架可以视为两层：上层是计算图，用于前向推理、自动微分和反向传播；下层是张量线性代数库，其负责底层的张量计算。在needle中，我们目前使用numpy作为线性代数库。本节我们将介绍一些常见的加速技术。

  • Vectorization 向量化 如果我们要将两个256长度的array相加，一种标量的处理方式是256个元素逐个相加，但是很多硬件都提供了批量从内存读取、向量运算指令，即优化为如下代码：
1
2
3
4
5
6
7
8

void vecadd(float* A, float* B, float* C){
	for(int i=0; i<64; i++){
		float4 a = load_float4(A + i*4);
		float4 b = load_float4(B + i*4);
		float4 c = add_float4(a, b);
		store_float4(C + i*4, c);
	}
}

这里要求ABC所在的内存块要是按照128 bit对齐的。

  • Data layout & strides 数据布局&步幅 在内存中，数据是线性排列的，因此一个矩阵在内存中有两种布局方式：行优先和列优先。一些古老的语言使用列优先，现代的语言偏向使用行优先。

在许多库中，还引入了一种stride格式布局，即在保存张量时，额外保存一个数据，用于标识每个维度上需要移动的步长。在这种情况下，a[i, j] = a_data[i * strides[0] + j * strides[1]]

这个方案可以在不用复制数据的情况下实现很多操作：通过改变offset和shape来实现切片；通过交换strides来实现转置；通过插入等于0的stride来实现广播。

其缺点是访存操作可能不再连续，因此向量化技术不可用，很多库也需要先把他们拼接之后再使用。

  • Parallelization 并行化 使用openmp可以将计算分配给多个核并行处理：
1
2
3
4
5
6
7
8
9

void vecadd(float* A, float* B, float* C){
	#pragma omp parallel for
	for(int i=0; i<64; i++){
		float4 a = load_float4(A + i*4);
		float4 b = load_float4(B + i*4);
		float4 c = add_float4(a, b);
		store_float4(C + i*4, c);
	}
}

Case study: matrix multiplication

本节我们将讨论如何优化矩阵乘法。

  • Vanilla matrix multiplication 朴素矩阵乘法 最朴素的想法是使用三重循环完成，其复杂度是$O(n^3)$，即如下代码：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

float A[n][n], B[n][n], C[n][n];

for(int i=0; i<n; i++){
	for(int j=0; j<n; j++){
		c[i][j] = 0;
		for(int k=0; k<n; k++){
		c[i][j] += A[i][k] * B[k][j];
		}
	}
}

在现代存储器中，L1 cache的速度比DRAM快200倍，通过优化数据的读取就可以显著提升计算速度，考虑到这一点，我们可以将中间变量保存到寄存器中，即：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

dram float A[n][n], B[n][n], C[n][n];

for(int i=0; i<n; i++){
	for(int j=0; j<n; j++){
		register float c = 0;
		for(int k=0; k<n; k++){
		register float a = A[i][k];
		register float b = B[k][j];
		c += a*b;
		}
		C[i][j] = c;
	}
}

上述代码中，从读取A、B到寄存器的操作分别进行了$n^3$次，需要3个寄存器来完成该操作。

  • Register tiled matrix multiplication 寄存器分块矩阵乘法 该方案的思路是将结果进行分块，每次计算其中的一块，即：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

dram float A[n/v1][n/v3][v1][v3];
dram float B[n/v2][n/v3][v2][v3];
dram float C[n/v1][n/v2][v1][v2];

for (int i = 0; i < n/v1; ++i) {
    for (int j = 0; j < n/v2; ++j) {
        register float c[v1][v2] = 0;
        for (int k = 0; k < n/v3; ++k) {
            register float a[v1][v3] = A[i][k];
            register float b[v2][v3] = B[j][k];
            c += dot(a, b.T);
        }
        C[i][j] = c;
    }
}

上述代码中，要计算的矩阵C被分为$v_1\times v_2$的小矩阵，为了计算出每一块，每次必须从A中选出$v_1$行，从B中选出$v_2$列，这两组子矩阵可以按照长度$v_3$再次划分。在计算中，前两个循环依次遍历C中的一小块，然后初始化$v_1 \times v_2$个寄存器用于保存该块内容，然后再根据$v_3$的大小二次划分，进行矩阵运算，将这些结果加到对应的寄存器上，第三个循环结束后就计算出C的一个子块。

A的数据加载开销是$n^3/v_2$，B的数据加载开销是$n^3/v_1$，A的寄存器开销是$v_1 \times v_3$，B的寄存器开销是$v_2\times v_3$，C的寄存器开销是$v_1\times v_2$。注意到$v_3$不影响数据加载的开销，因此可以取$v_3$为1，然后在满足寄存器总数约束的情况下，最大化$v_1$和$v_2$。

之所以能够减小开销是因为在矩阵计算中，元素被重复使用，通过每次计算一个分块的方式，可以保证这个分块内用到的重复数据只要加载一次。

  • Cache line aware tiling 缓存行感知分块 前面我们使用寄存器来进行加速，本节我们考虑使用cache来加速。我们的实现代码为：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

dram float A[n/b1][b1][n];
dram float B[n/b2][b2][n];
dram float C[n/b1][n/b2][b1][b2];

for (int i = 0; i < n/b1; ++i) {
    l1cache float a[b1][n] = A[i];
    for (int j = 0; j < n/b2; ++j) {
        l1cache float b[b2][n] = B[j];
        
        C[i][j] = dot(a, b.T);
    }
}

上述代码中，结果矩阵C被分块为$b_1 \times b_2$，A和B分别按行和按列分块，通过两层循环遍历计算C中的每个子块，计算子块的过程可以使用寄存器分块进行加速。

上述代码中，A的加载开销是$n^2$，B的加载开销是$n^3/b1$。有两个约束，一个是$b_1n+b_2n < \text{l1 chche size}$，另一个是$b_1 % v_1=b_2 % v_2 = 0$。

  • Put it together 将缓存版本的dot运算使用寄存器版本展开，可以得到最终的分块乘法实现：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

dram float A[n/b1][b1/v1][n][v1];
dram float B[n/b2][b2/v2][n][v2];

for (int i = 0; i < n/b1; ++i) {
    l1cache float a[b1/v1][n][v1] = A[i];
    for (int j = 0; j < n/b2; ++j) {
        l1cache b[b2/v2][n][v2] = B[j];
        for (int x = 0; x < b1/v1; ++x)
            for (int y = 0; y < b2/v2; ++y) {
                register float c[v1][v2] = 0;
                for (int k = 0; k < n; ++k) {
                    register float ar[v1] = a[x][k][:];
                    register float br[v2] = b[y][k][:];
                    C += dot(ar, br.T)
                }
            }
    }
}

上述代码的数据加载开销是：

$$ speed_{l1}\cdot(\frac{n^3}{v_2}+\frac{n^3}{v1})+speed_{dram}\cdot(n^2+\frac{n^3}{b_1}) $$

Lecture 12: GPU acceleration

GPU programming

如下图所示，CPU是一种通用处理器，其可以灵活地处理不同的任务，每个核都有独立的控制器。但在某些任务，例如图形渲染中，可能存在大量的重复工作，例如给每个像素都进行相同的处理。GPU正是擅长处理此类任务，其有大量的执行单元，可以批量执行同一指令。将GPU应用于深度学习，可以带来10X ~ 100X的加速倍率。 image.png

  • GPU programming model: SIMT 在本章节，我们将使用CUDA中的术语，但是在别的模型中，通常也有对应的概念。

SIMT中所有的线程都执行相同的指令，但是具有不同的数据通路。线程被分组为block，每个block共享内存。block被分组为launch grid，当启动一个kernel时，实际上就是在一个grid上执行。

  • Example: vector add 以下代码演示了在CPU和GPU上执行向量加法的过程：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

void VecAddCPU(float* A, float *B, float* C, int n) {
    for (int i = 0; i < n; ++i) {
        C[i] = A[i] + B[i];
    }
}

__global__ void VecAddKernel(float* A, float *B, float* C, int n) {
    int i = blockDim.x * blockIdx.x + threadIdx.x;
    if (i < n) {
        C[i] = A[i] + B[i];
    }
}

从GPU版本我们可以看到，每个线程执行的指令都是相同，不同的是每个线程具有不同的环境变量。

为了执行上述GPU代码，在主机端要执行以下内容：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

void VecAddCUDA(float *Acpu, float *Bcpu, float *Ccpu, int n) {
    float *dA, *dB, *dC;
    cudaMalloc(&dA, n * sizeof(float));
    cudaMalloc(&dB, n * sizeof(float));
    cudaMalloc(&dC, n * sizeof(float));

    cudaMemcpy(dA, Acpu, n * sizeof(float), cudaMemcpyHostToDevice);
    cudaMemcpy(dB, Bcpu, n * sizeof(float), cudaMemcpyHostToDevice);

    int threads_per_block = 512;
    int nblocks = (n + threads_per_block - 1) / threads_per_block;
    VecAddKernel<<<nblocks, threads_per_block>>>(dA, dB, dC, n);

    cudaMemcpy(Ccpu, dC, n * sizeof(float), cudaMemcpyDeviceToHost);

    cudaFree(dA);
    cudaFree(dB);
    cudaFree(dC);
}

函数的输入是来自cpu内存上的三个数组，在GPU上分配出对应大小的显存，然后将两个加数拷贝到设备中。根据数据的规模确定要启用的block数量，然后执行GPU代码，最后将结果拷贝会CPU内存并释放相应显存。

在实际中，内存拷贝是一个非常耗时的过程，因此我们希望将数据一直保留在显存中进行计算，而非频繁地来回拷贝。

  • Example: window sum window sum是一种权重全为1的卷积，一种朴素的想法是这么些的：
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

#define RADIUS 2

__global__ void WindowSumSimpleKernel(float* A, float *B, int n) {
    int out_idx = blockDim.x * blockIdx.x + threadIdx.x;
    if (out_idx < n) {
        float sum = 0;
        for (int dx = -RADIUS; dx <= RADIUS; ++dx) {
            sum += A[dx + out_idx + RADIUS];
        }
        B[out_idx] = sum;
    }
}

但显然，这个算法并不高效，将重复访问数据，要加载$5n$次数据。

这时候可以引入共享内存进行优化，将一个block内要要用到的数据全部读取到共享内存中。数据加载的任务可以分给每个线程并行完成，显著降低了内存加载时间开销。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

__global__ void WindowSumSharedKernel(float* A, float* B, int n) {
    __shared__ float temp[THREADS_PER_BLOCK + 2 * RADIUS];
    int base = blockDim.x * blockIdx.x;
    int out_idx = base + threadIdx.x;
    if (base + threadIdx.x < n) {
        temp[threadIdx.x] = A[base + threadIdx.x];
    }
    if (threadIdx.x < 2 * RADIUS && base + THREADS_PER_BLOCK + threadIdx.x < n) {
        temp[threadIdx.x + THREADS_PER_BLOCK] = A[base + THREADS_PER_BLOCK + threadIdx.x];
    }
    __syncthreads();
    if (out_idx < n) {
        float sum = 0;
        for (int dx = -RADIUS; dx <= RADIUS; ++dx) {
            sum += temp[threadIdx.x + dx + RADIUS];
        }
        B[out_idx] = sum;
    }
}

通过__syncthreads同步，确保所有线程都将数据加载完毕，然后再计算window sum。

Case study: matrix multiplication on GPU

从线程的细粒度来说，我们可以在GPU上实现一个寄存器分块版本的矩阵乘法：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

__global__ void mm(float A[N][N], float B[N][N], float C[N][N]) {
    int ybase = blockIdx.y * blockDim.y + threadIdx.y;
    int xbase = blockIdx.x * blockDim.x + threadIdx.x;

    float c[V][V] = {0};
    float a[V], b[V];
    for (int k = 0; k < N; ++k) {
        a[:] = A[k, ybase*V : ybase*V + V];
        b[:] = B[k, xbase*V : xbase*V + V];
        for (int y = 0; y < V; ++y) {
            for (int x = 0; x < V; ++x) {
                c[y][x] += a[y] * b[x];
            }
        }
    }
    C[ybase * V : ybase * V + V, xbase * V : xbase * V + V] = c[:,:];
}

每个线程负责计算一个分块的结果，即每次计算下图中的一块。 image.png 还可以将计算一块的任务交给一个block，这样就可以使用共享内存技术有block内的线程共同加载要用到的数据。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

__global__ void mm(float A[N][N], float B[N][N], float C[N][N]) {
    __shared__ float sA[S][L], sB[S][L];
    float c[V][V] = {0};
    float a[V], b[V];
    int yblock = blockIdx.y;
    int xblock = blockIdx.x;

    for (int ko = 0; ko < N; ko += S) {
        __syncthreads();
        // needs to be implemented by thread cooperative fetching
        sA[:, :] = A[ko + S, yblock * L : yblock * L + L];
        sB[:, :] = B[ko + S, xblock * L : xblock * L + L];
        __syncthreads();

        for (int ki = 0; ki < S; ++ki) {
            a[:] = sA[ki, threadIdx.x * V + V];
            b[:] = sB[ki, threadIdx.x * V + V];
            for (int y = 0; y < V; ++y) {
                for (int x = 0; x < V; ++x) {
                    c[y][x] += a[y] * b[x];
                }
            }
        }
    }

    int ybase = blockIdx.y * blockDim.y + threadIdx.y;
    int xbase = blockIdx.x * blockDim.x + threadIdx.x;
    C[ybase * V : ybase * V + V, xbase * V : xbase * V + V] = c[:, :];
}

上述代码从全部内存到共享内存的加载过程被复用L次（计算每个分块矩阵都要读取L次AB的行列向量），从共享内存到寄存器被复用V次（在分块矩阵中按照长度V进行了二次分块计算） image.png 各线程读取数据到共享内存的过程为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

sA[:, :] = A[k : k + S, yblock * L : yblock * L + L];


int nthreads = blockDim.y * blockDim.x;
int tid = threadIdx.y * blockDim.x + threadIdx.x;
for(int j = 0; j < L * S / nthreads; ++j) {
    int y = (j * nthreads + tid) / L;
    int x = (j * nthreads + tid) % L;
    s[y, x] = A[k + y, yblock * L + x];
}

Lecture 13: Hardware Acceleration Implemetation

这节是实验课，在这节课中，我们将学习needle库中CPU和GPU底端具体实现的代码骨架。

这节课不做笔记，本节课内容可通过完成hw3学习。

Lecture 14: Implementing Convolutions

本节课将学习卷积算子的具体实现。

存储格式 Storage Order

对于图片数据或者隐藏层，我们需要存储batch_size*channel*height*width即B*C*H*W个元素，本课程中，我们选取的存储格式为：

1

float Z[BATCHES][HEIGHT][WIDTH][CHANNELS];

上述格式被称为NHWC格式（N代表number）。PyTorch默认格式为NCHW，其在后期版本也支持NHWC。不同的格式会影响操作的性能：卷积在NHWC上更快，Batch Norm在NCHW上更快。

对于卷积核，其需要存储k*k*C_in*C_out个元素，本课程我们选取的存储格式为：

1

float weights[KERNEL_SIZE][KERNEL_SIZE][IN_CHANNELS][OUT_CHANNELS];

PyTorch选择的格式为(C_out, C_in, k, k)。

for循环实现卷积 Convolutions with simple loops

通过循环来实现卷积操作的过程，从外到内，循环迭代的参数依次为：batch、channel_in、channel_out、out_row、out_column，还有两个循环用于实现卷积，共七个循环：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def conv_naive(Z, weight):
    N,H,W,C_in = Z.shape
    K,_,_,C_out = weight.shape
    
    out = np.zeros((N,H-K+1,W-K+1,C_out));
    for n in range(N):
        for c_in in range(C_in):
            for c_out in range(C_out):
                for y in range(H-K+1):
                    for x in range(W-K+1):
                        for i in range(K):
                            for j in range(K):
                                out[n,y,x,c_out] += Z[n,y+i,x+j,c_in] * weight[i,j,c_in,c_out]

该七重循环实现的卷积耗时3秒，而PyTorch仅需1.2毫秒，约2500倍的性能差距。

矩阵乘法实现卷积 Convolutions as matrix multiplications

卷积核中任意一个元素[ i, j, :, : ]都是一个shape为(c_in, c_out)的矩阵，当其作用在输入图片的某个元素(p,q,m,:)即作用在一个长度为c_in的向量上时，这个过程就是一个矩阵乘法运算。

特别的，对于卷积核大小为1×1的情况，整个卷积过程可以直接用一个矩阵乘法来表示：

1
2

W1 = np.random.randn(1,1,8,16)
out = conv_reference(Z,W1)

怎么将1×1的卷积核推广到一般情况呢？可以把卷积核看成由一个个1×1的小卷积核组成的，不断迭代这些卷积核即可。需要注意的是，每个小卷积核在图片上作用的范围都不一样，要做好切片：

1
2
3
4
5
6
7
8
9

def conv_matrix_mult(Z, weight):
    N,H,W,C_in = Z.shape
    K,_,_,C_out = weight.shape
    out = np.zeros((N,H-K+1,W-K+1,C_out))
    
    for i in range(K):
        for j in range(K):
            out += Z[:,i:i+H-K+1,j:j+W-K+1,:] @ weight[i,j]
    return out

该版本卷积耗时17毫秒，相比PyTorch1.2毫秒，约14倍性能差距。

通过strides来操作矩阵 Manipulating matrices via strides

在内存中，通常将矩阵按照二维数组的形式在内存中存储：

1

float A[M][N];

但是，我们在实现一些高效算子时，经常会把矩阵分块，如果将其分块存储，那么这些算子将会具有更好的空间局部性：

1

float A[M/TILE][N/TILE][TILE][TILE]

NumPy提供了一个函数用于实现从二维数组转变为分块矩阵的格式：np.lib.stride_tricks.as_strided4。

具体来说，as_strided这个函数用于创建一个具有不同shape和strides，但与原array具有相同底层数据的视图（view）。

举个例子，如下图所示，一个6×6的矩阵，对于按照2×2进行分块，我们从strides[3]倒着写出其值。 image.png

  • strides [3]表示在子矩阵内部移动到下一列的元素的步长，即从0移动到1的步长，数据在内存中是按行连续排列的，因此其值为1；
  • strides [2]表示在子矩阵中移动到下一行元素的步长，即从0移动到6的所需步长，观察图片可以看到该步步长等于矩阵的列数N，即6；
  • strides [1]表示从一个子矩阵移动到同行下一个子矩阵的对应位置的步长，即从0移动到2的步长，可以看到移动的步长等于分块的列长度TILE，即2；
  • strides [0]表示从一个子矩阵移动到同列下一个子矩阵对应位置的步长，即从0移动到12的步长，可以看到移动的步长等于TILE*N，即12。

确定了strides之后，就可以使用as_strided为原矩阵创建一个分块矩阵的视图，并使用np.ascontiguousarray创建一个内存连续版本的副本：

1
2
3
4
5
6

import numpy as np
n = 6
A = np.arange(n**2, dtype=np.float32).reshape(n,n)

B = np.lib.stride_tricks.as_strided(A, shape=(3,3,2,2), strides=np.array((12,2,6,1))*4)  #numpy中strides以字节为单位
C = np.ascontiguousarray(B)

—————-以下非课程内容—————- 这里插一嘴，这里实现分块的方式非常不优雅，毕竟numpy并不建议使用这么底层的API来直接修改数据，我问了下GPT，他提供了一种更优雅的方案。

我们首先可以将原矩阵(M, N)reshape为(M//TILE, TILE, N//TILE, TILE)，这一步相当于将原矩阵在行和列上进行分块，并且(p,m,q,n)表示第p行第q列的子矩阵中第m行第n列个元素。然后使用transpose(0, 2, 1, 3)重新排列维度即可。

至于为什么reshape那一步后索引仍是正确的，我略微理解的，但难以表达出来，有点只可意会的意思：reshape那个操作可以分成两步完成，分别是在行和列上进行切片，这两个步骤又不冲突，合并后的结果就是如下的代码：

1
2
3
4
5
6

def block_matrix(A, TILE):
    M, N = A.shape
    assert M % TILE == 0 and N % TILE == 0, "矩阵维度必须能被TILE整除"
    A_reshaped = A.reshape(M//TILE, TILE, N//TILE, TILE)
    A_blocked = A_reshaped.transpose(0, 2, 1, 3)
    return np.ascontiguousarray(A_blocked)

—————-以上非课程内容—————-

通过 im2col 来实现卷积 Convolutions via im2col

在Lecture 10中提到，我们可以使用im2col技术，将一维卷积运算转换为矩阵运算：

$$ \begin{bmatrix}z_1\\z_2\\z_3\\z_4\\z_5\end{bmatrix}=x*w=\begin{bmatrix}0&x_1&x_2\\x_1&x_2&x_3\\x_2&x_3&x_4\\x_3&x_4&x_5\\x_4&x_5&0\end{bmatrix}\begin{bmatrix}w_1\\w_2\\w_3\end{bmatrix} $$
对于二维卷积来说，同样也是可以的。以卷积核大小为3×3为例，对6×6的矩阵进行卷积，其结果矩阵为4×4。首先，我们找出每次运算的感受野，将其单独拿出来，那么所有这些感受野就组成了一个4×4×3×3的Tensor。

如下图所示，第[0,0]个感受野就是[0,1,2;6,7,8;12,13,14]。怎么将原始矩阵转变为Tensor呢？这里就可以用到上节提到的as_strided方法。strides[0]表示到同列下一个感受野的相同位置的元素的步长，为列长6；strides[1]表示到同行下一个感受野的步长，为1；strides[2]表示同一个感受野内部同列下一个元素的步长，为原始列长6；strides[3]表示同一个感受野内部同行下一个元素的步长，为1。即，使用B = np.lib.stride_tricks.as_strided(A, shape=(4,4,3,3), strides=4*(np.array((6,1,6,1))))可以将原始待卷积矩阵A转变为感受野张量B。 image.png

下一步，通过reshape操作将单个感受野和卷积核都转变为向量，通过内积运算计算卷积值：

1

(B.reshape(16,9) @ W.reshape(9)).reshape(4,4)

需要注意的是，B的reshape的操作并不是free的，无法通过原始的A的数据来表示reshape后的B，该reshape操作会分配出一块$O(K^2)$的内存空间，当K比较大时，这个操作将相当耗费内存。因此，在现代版本中，常常会使用lazy技术或者其它技术，但这不在本课程讨论范围之内。

通过 im2col 来实现多通道卷积

对于多通道并且考虑batch的卷积，其输入shape为N×H×W×C_in，感受野Tensor为N×(W-K+1)×(H-K+1)×K×K×C_in，需要将K×K×C_in展开为一维，卷积核也要将对应位置展开，即reshape后shape为(K×K×C_in)×C_out。

代码实现为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def conv_im2col(Z, weight):
    N,H,W,C_in = Z.shape
    K,_,_,C_out = weight.shape
    Ns, Hs, Ws, Cs = Z.strides
    
    inner_dim = K * K * C_in
    A = np.lib.stride_tricks.as_strided(Z, shape = (N, H-K+1, W-K+1, K, K, C_in),
                                        strides = (Ns, Hs, Ws, Hs, Ws, Cs)).reshape(-1,inner_dim)
    out = A @ weight.reshape(-1, C_out)
    return out.reshape(N,H-K+1,W-K+1,C_out)

Lecture 15: Training Large Models

内存节省技术 Techniques for memory saving

一直以来，GPU的全局内存大小都是模型大小的制约瓶颈，通过一些内存节省技术可以训练更大的一些模型。

模型内存消耗主要有如下几个方面：模型权重、优化器状态（动量值等等）、中间激活层的值。

对于推理来说，保存激活层的内存只需要两块，分别用来保存一层的输入和输出，下一层的输入为上一层的输出，下一层的输出覆盖上一层的输入。其不需要保存中间激活层的值。

而在训练中，由于在计算每一层的梯度时都用到了该层的输入，所每一个激活层都要一片内存保存下来，即激活层的内存数量为$O(N)$，如下图所示： image.png

一种减少激活层内存使用的技术叫做checkpoint，就是每隔一个激活层才保存该层的值，如下图所示： image.png 在反向传播时，如果需要用到未保存的隐藏层，则通过上一个隐藏层计算出该层的值即可。这是一种时间换空间的思路。对于一个N层的网络，每隔K个隐藏层保存一次结果，则隐藏层占用的内存空间大小为$O(N/K)+O(K)$，当$K=\sqrt{N}$时可取到最小值。

并行和分布式训练 Parallel and distributed training

  • 计算图划分

当有多个GPU时，可以进行并行分布式训练。一种思路是将计算图进行划分，并分配给不同的worker进行执行，通过通讯协议在worker中间传递数据。如下图所示，整个计算图被划分为两部分。 image.png 仅仅将计算图划分并不会带来多少的并行性，但是当worker1计算来自worker0的数据时，worker0可以并行计算下一个minibatch的数据，从而实现高并行。

  • 数据并行训练

数据并行训练是的是将一个minibatch分割成更小的smaller batch，每个GPU负责一个smaller batch的计算，这样做每隔GPU上都在跑相同的模型。

在分布式和并行计算中，有一个allreduce原语，其作用是将分布在多个进程或节点上的数据进行规约（reduction）操作，然后将结果广播回所有参与的进程或节点。运用这个原语，我们可以在多GPU上计算出smaller batch的梯度，然后利用该原语将计算出整个minibatch的梯度并进行梯度下降。

我们还可以将参数使用专门的参数服务器保存，其它设备需要访问或者更新参数时，只需要调用相应API即可。参数服务器的好处是其不需要等待所有的worker都计算结束再更新，支持动态增减worker数量，提高了系统的鲁棒性。

  • 通信计算重叠 communication computation overlap

通信计算重叠，就是指在通信同步时使用非阻塞的方式，在等待IO时继续计算。

Lecture 16 Generative Adversarial Network

生成对抗训练 Generative adversarial training

对于无监督学习，或者称生成式模型，其任务是通过随机向量生成符合数据集分布的样本。这就引入了一个问题：如何评估样本和目标分布之间的距离。这一评价指标作为我们的目标函数，其必须是可微的，以便后续对模型进行优化。

对抗训练的思路是构造一个oracle classfier D，其作用是辨别生成数据和原始数据，D的输出是输入为生成数据为生成数据的概率。那对于任意一个输入z，生成网络G的输出为G(z)，D对其的判别结果为D(G(z))。那生成器的目标就是尽可能让判别器判别错误，即其损失函数为：

$$ \max_G\{-E_{z\sim Noise}\log{(1-D(G(z)))}\} $$

需要注意的是，这里并没有现成的辨别器D。我们同样可以用一个神经网络来构造这个辨别器，那这个辨别器的目标就是尽可能判断正确，即其损失函数为：

$$ \min_D\{-E_{z\sim Noise}\log{(1-D(G(z)))}-E_{x\sim Data}\log{D(x)}\} $$

将对抗训练作为深度学习中的一个模块 Adversarial training as a module in deep learning models

接下来我们考虑如何将对抗模型模块化。我们可以将整个判别器作为一个损失函数来实现，当然，其和我们之前实现的损失函数是不一样的，判别器的参数在每轮反向传播时都要更新。

【这一节课似乎没有具体说明如何模块化，后边似乎在介绍GAN网络的各个变种】

在DCGAN中，使用了一种被称为反卷积（转置卷积、Conv2dTranspose）的模块，其作用是进行上采样。

CycleGAN是一个用于风格迁移的模型。对于风格迁移模型来说，一种有监督的训练思路是收集风格迁移前后的图片配对数据集，进行有监督训练。然而，此类配对数据集是很难获取的。如何通过未配对的数据集进行无监督训练呢？可以使用GAN网络，一个生成器G用于升成风格迁移后的图片，使用一个判别器进行对抗训练。另外有一个生成器F，用于还原图片，其也使用一个判别器进行对抗训练。而整个CycleGAN模型还需要保证循环一致性，即将数据集中的一个图片经过G之后，再经过F，应当还原成原始图片，故循环一致性的损失函数就是两个图片之间的L2 Norm。

在下节课中，将讨论GAN系列网络的具体实现。

Lecture 17: Generative Adversarial Networks implementations

本节课中，我们将学习GAN网络的具体实现。

在课程中，使用二维高斯分布作为真实数据集，训练一个生成器用于升成该分布的数据。训练集数据准备如下：

1
2
3
4
5

A = np.array([[1, 2], [-0.2, 0.5]])
mu = np.array([2, 1])
# total number of sample data to generated
num_sample = 3200
data = np.random.normal(0, 1, (num_sample, 2)) @ A + mu

生成器使用一个简单的全连接层即可：

1
2
3
4
5
6

model_G = nn.Sequential(nn.Linear(2, 2))

def sample_G(model_G, num_samples):
    Z = ndl.Tensor(np.random.normal(0, 1, (num_samples, 2)))
    fake_X = model_G(Z)
    return fake_X.numpy()

判别器是一个三层的感知机，损失函数为softmax loss：

1
2
3
4
5
6
7
8

model_D = nn.Sequential(
    nn.Linear(2, 20),
    nn.ReLU(),
    nn.Linear(20, 10),
    nn.ReLU(),
    nn.Linear(10, 2)
)
loss_D = nn.SoftmaxLoss()

优化生成器G的过程就是使用G随机生成一些数据G(z)，计算D(G(z))的输出和label 1之间的损失：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

opt_G = ndl.optim.Adam(model_G.parameters(), lr=0.01)、

def update_G(Z, model_G, model_D, loss_D, opt_G):
    fake_X = model_G(Z)
    fake_Y = model_D(fake_X)
    batch_size = Z.shape[0]
    ones = ndl.ones(batch_size, dtype="int32")
    loss = loss_D(fake_Y, ones)
    loss.backward()
    opt_G.step()

同样，判别器的更新过程就是计算D(x)和label 1之间的损失，D(G(z))和label 0之间的损失，x是真实数据：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

opt_D = ndl.optim.Adam(model_D.parameters(), lr=0.01)

def update_D(X, Z, model_G, model_D, loss_D, opt_D):
    fake_X = model_G(Z).detach()
    fake_Y = model_D(fake_X)
    real_Y = model_D(X)
    assert X.shape[0] == Z.shape[0]
    batch_size = X.shape[0]
    ones = ndl.ones(batch_size, dtype="int32")
    zeros = ndl.zeros(batch_size, dtype="int32")
    loss = loss_D(real_Y, ones) + loss_D(fake_Y, zeros)
    loss.backward()
    opt_D.step()

训练过程则是每次迭代中，将随机向量送入生成器，再将生成器的输出喂给判别器，然后分别更新二者的参数即可，注意以下代码中epoch指的是训练了几个batch，而不是指在训练集上完整训练了几轮：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def train_gan(data, batch_size, num_epochs):
    assert data.shape[0] % batch_size == 0
    data.astype(np.float32)
    for epoch in range(num_epochs):
        begin = (batch_size * epoch) % data.shape[0]
        X = data[begin: begin+batch_size, :]
        Z = np.random.normal(0, 1, (batch_size, 2))
        X = ndl.Tensor(X)
        Z = ndl.Tensor(Z)
        update_D(X, Z, model_G, model_D, loss_D, opt_D) 
        update_G(Z, model_G, model_D, loss_D, opt_G)

train_gan(data, 32, 2000)

以上就是训练一个GAN网络的全过程，接下来我们考虑如何GAN Loss模块化。GAN Loss的作用是给定一个生成器的输出，返回一个损失值。此外，当生成器拿到损失值后就会直接进行生成器的参数更新，因此GAN Loss内部必须隐式更新自身的参数，即：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class GANLoss:
    def __init__(self, model_D, opt_D):
        self.model_D = model_D
        self.opt_D = opt_D
        self.loss_D = nn.SoftmaxLoss()

    def _update_D(self, real_X, fake_X):
        real_Y = self.model_D(real_X)
        fake_Y = self.model_D(fake_X.detach())
        batch_size = real_X.shape[0]
        ones = ndl.ones(batch_size, dtype="float32")
        zeros = ndl.zeros(batch_size, dtype="float32")
        loss = self.loss_D(real_Y, ones) + self.loss_D(fake_Y, zeros)
        loss.backward()
        self.opt_D.step()

    def forward(self, fake_X, real_X):
        self._update_D(real_X, fake_X)
        fake_Y = self.model_D(fake_X)
        batch_size = real_X.shape[0]
        ones = ndl.ones(batch_size, dtype="float32")
        loss = self.loss_D(fake_Y, ones)
        return loss

Lecture 18: Sequence Modeling and Recurrent Networks

序列建模 Sequence modeling

在前面的模型中，我们都做了一个隐式假设：x和y之间是独立同分布的，但是在实践中，很多任务的y都是与x相关的，尤其是当y是一个时间序列数据。

对于序列数据来说，有一类预测模型是自回归模型，其基本思想是利用序列自身的历史值来预测未来值。

循环神经网络 Recurrent neural networks

循环网络也能用于解决序列数据的建模问题。RNN网络的思想是构建一个网络模型用于模拟输入序列中的时序信息。

如下图所示，h表示模型中的隐藏层，隐藏层的输入为前一个隐藏层的状态和当前输入x，经过非线性变换后得到该隐藏层，当前输入的对应输出则由对应隐藏层经过非线性变换后得到。 即：

$$ \begin{align*} h_t &= f(h_{t-1},x_t)\\ y_t &=g(h) \end{align*} $$

image.png

理论上来说，如果建模得当，这种模式在预测$y_t$时可以获取前面所有时刻的时序信息。

RNN的训练时需要配对的x和y作为数据集，损失函数由每一个预测值和真实值之间的损失累加得到。显然，这个损失函数很难通过笔纸进行推导，但得益于我们之前构建的自动微分系统，我们不需要手动计算任何梯度。

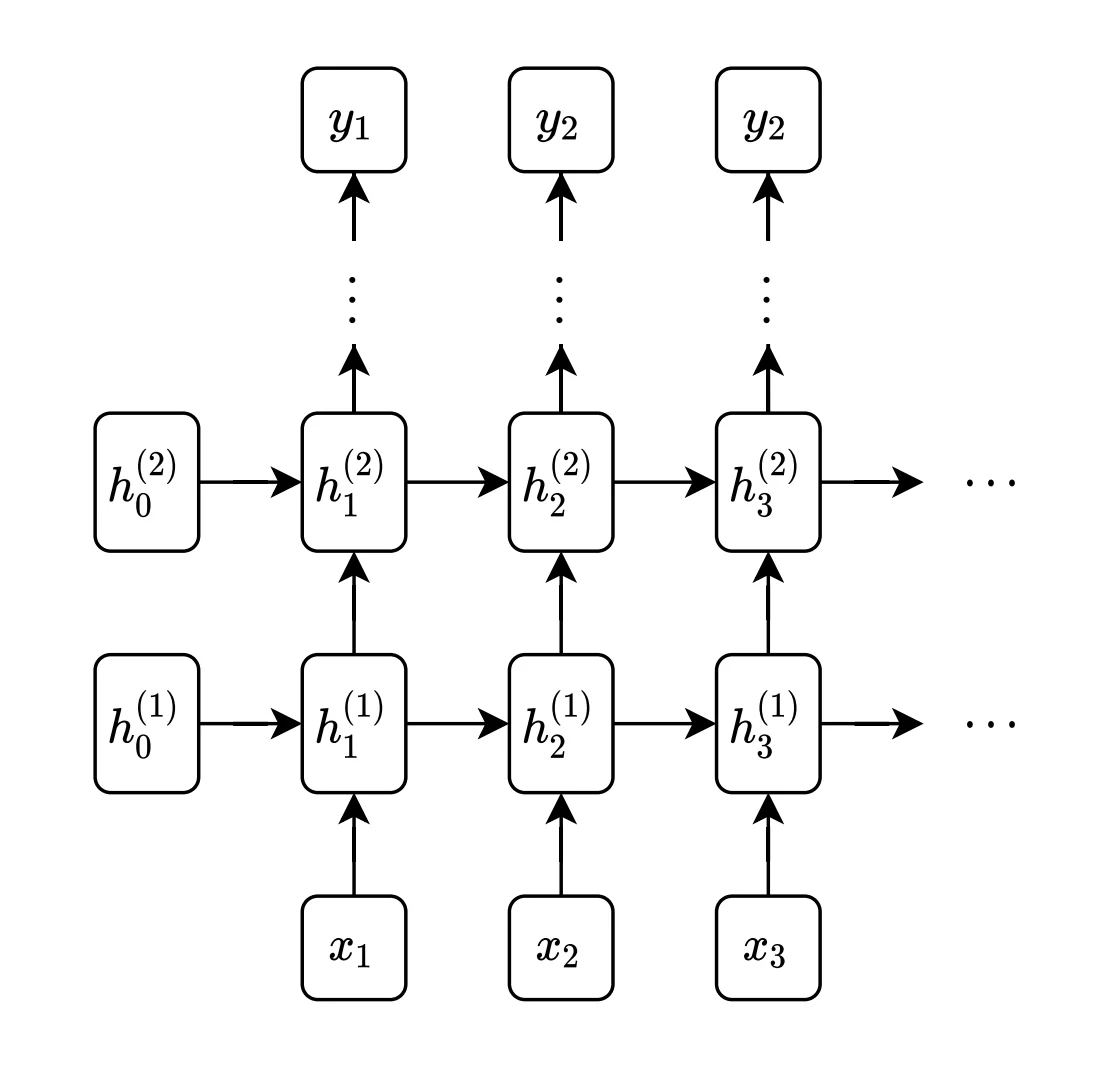
可以将多个RNN堆叠在一起，得到stacking RNN，如下图所示： image.png

RNN在训练过程中很容易出现梯度/激活层爆炸和梯度/激活层消失问题。之前的lecture提到，当训练很深的网络时，初始化参数是很重要的。在RNN上，这个问题更加严重，因为RNN的模型通常很深很深。

一个解决梯度问题的方法是着眼于激活函数。ReLU作为激活函数其一个问题是其输出可以无限大。然而，将激活函数修改为有界函数，例如sigmoid或者tanh并不能解决这一问题，尤其是，其不能解决激活层/梯度消失问题。如下所示，对于tanh，当x在0附近时，其输出仍在0附近，这会导致隐藏层消失；但于两个函数，当输入在-5和5附近时，其梯度很小，这会导致梯度消失。

image.png

LSTMs

LSTM一定程度上减轻了RNN中存在的梯度消失和爆炸问题。LSTM在原版RNN的基础上对隐藏层进行了一定改进。如下图所示，LSTM将原始hidden state分裂为两个组件hidden state和cell state。 image.png

其次，LSTM中具体定义了hidden state和cell state的具体更新公式。LSTM中定义了一些中间变量用于更简洁地描述这一公式，中间变量有forget gate、input gate、output gate，还有一个候选状态g_t。这些中间变量和状态的更新公式如下所示：

$$ \begin{align*} &\begin{bmatrix}i_t\\f_t\\g_t\\o_t\end{bmatrix}=\begin{pmatrix}\text{sigmoid}\\\text{sigmoid}\\\text{tanh}\\\text{sigmoid}\end{pmatrix}(W_{hh}h_{t-1}+\text{W}_{hx}x_t+b_h) \\ &c_t=c_{t-1}\circ f_t+i_t\circ g_t \\ &h_t=\tanh(c_t)\circ o_t\\ &i_t,f_t,g_t,o_t,c_t,h_t \in \mathbb{R}^d\\ &W_{hh},W_{hx}\in \mathbb{R}^{4d\times d} \end{align*} $$

$W_{hh},W_{hx}\in \mathbb{R}^{4d\times d}$意味着，计算中间变量的权重彼此都是独立的。

？？？？！！！这公式怎么来的，为啥子这个公式管用？有很多工作试图对此进行解释，但大多是一家之言。Zico Kolter教授对此的解释是：$g_t$在经过sigmoid以后是一个0-1变量，用于决定是否要保留前一状态对应位置的cell state信息，$i_t$同样是个0-1变量，而$g_t$是个有界项，这一组合决定了是否要在cell state的位置上添加一些额外的信息；$h_t$的更新公式则是一个有界变量，其作用是防止梯度爆炸或者消失。

Beyond “simple” sequential models

除了对序列数据进行建模，RNN能做的还有很多。例如，翻译句子，有一种sequence to sequence架构采用了两个RNN模型，一个用于输入原始句子，提取中间状态，另一个用于根据最后一个中间状态，输出翻译后的句子。 image.png

这意味着，RNN可以作为一个encoder对语义信息进行提取和编码，也可以作为decoder对语义信息进行解码。

RNN有一种变体是双向RNN，其作用是$x_i$时刻的输出与前后都相关，在一些任务，例如完形填空中可以有较好的表现。

Lecture 19: LSTM Implementation

LSTM cell

本节课，我们将在NumPy实现LSTM。首先来实现LSTM cell，一个cell是hidden state和cell state的集合，其状态更新公式为：

$$ \begin{align*} \\ i_t &= \sigma(W_{ii} x_t + b_{ii} + W_{hi} h_{t-1} + b_{hi}) \\ f_t &= \sigma(W_{if} x_t + b_{if} + W_{hf} h_{t-1} + b_{hf}) \\ g_t &= \tanh(W_{ig} x_t + b_{ig} + W_{hg} h_{t-1} + b_{hg}) \\ o_t &= \sigma(W_{io} x_t + b_{io} + W_{ho} h_{t-1} + b_{ho}) \\ c_t &= f_t \odot c_{t-1} + i_t \odot g_t \\ h_t &= o_t \odot \tanh(c_t) \\ \end{align*} $$

上述公式在上节课中，可以记为矩阵的形式，即：

$$ \begin{align*} &\begin{bmatrix}i_t\\f_t\\g_t\\o_t\end{bmatrix}=\begin{pmatrix}\text{sigmoid}\\\text{sigmoid}\\\text{tanh}\\\text{sigmoid}\end{pmatrix}(W_{hh}h_{t-1}+\text{W}_{hx}x_t+b_h) \\ &c_t=c_{t-1}\circ f_t+i_t\circ g_t \\ &h_t=\tanh(c_t)\circ o_t\\ &i_t,f_t,g_t,o_t,c_t,h_t \in \mathbb{R}^d\\ &W_{hh},W_{hx}\in \mathbb{R}^{4d\times d} \end{align*} $$

在PyTorch中，已经有LSTM的具体实现，当我们实例化一个$20\times100$的cell，即输入向量长度为20，中间状态特征长度为100，那$W_{hh}$和$W_{hx}$的形状就是$400\times 100$和$400\times 20$。

根据上述更新公式，可以得到计算一个LSTM cell 的方法：

1
2
3
4
5
6
7
8
9

def sigmoid(x):
    return 1/(1+np.exp(-x))

def lstm_cell(x, h, c, W_hh, W_ih, b):
    i,f,g,o = np.split(W_ih@x + W_hh@h + b, 4)
    i,f,g,o = sigmoid(i), sigmoid(f), np.tanh(g), sigmoid(o)
    c_out = f*c + i*g, 
    h_out = o * np.tanh(c_out)
    return h_out, c_out

Full sequence LSTM

基于PyTorch的传统，在实现LSTM时，返回所有的hidden state以及最后一个cell state。前面没有提到，LSTM中各个cell的参数的权重是共享的。那LSTM实际上就是根据序列的长度重复执行lstm_cell即可：

1
2
3
4
5
6

def lstm(X, h, c, W_hh, W_ih, b):
    H = np.zeros((X.shape[0], h.shape[0]))
    for t in range(X.shape[0]):
        h, c = lstm_cell(X[t], h, c, W_hh, W_ih, b)
        H[t,:] = h
    return H, c

Batching efficiently

接下来我们考虑如何实现batch LSTM，一种符合习惯的做法是将batch作为第一个维度将输入X堆叠起来，即X[NUM_BATCHES][NUM_TIMESTEPS][INPUT_SIZE]，这种格式被称为NTC格式。如果采用改格式，那么在经过lstm时，第i个cell访问的元素为X[:,i,:]，注意，这些元素在内存中不是紧密排列的，cache命中率较低。

如果将时间维度放在第一个，即采用TNC格式，则能够解决该问题。

其余代码几乎不需要改动，矩阵乘法时要注意将三维的X放到@运算符前面：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

def lstm_cell(x, h, c, W_hh, W_ih, b):
    i,f,g,o = np.split(x@W_ih + h@W_hh + b[None,:], 4, axis=1)
    i,f,g,o = sigmoid(i), sigmoid(f), np.tanh(g), sigmoid(o)
    c_out = f*c + i*g
    h_out = o * np.tanh(c_out)
    return h_out, c_out

def lstm(X, h, c, W_hh, W_ih, b):
    H = np.zeros((X.shape[0], X.shape[1], h.shape[1]))
    for t in range(X.shape[0]):
        h, c = lstm_cell(X[t], h, c, W_hh, W_ih, b)
        H[t,:,:] = h
    return H, c

Training LSTMs

训练一个单层LSTM很简单，不赘述，直接看代码：

1
2
3
4
5

def train_lstm(X, Y, h0, c0, parameters)
    H, cn = lstm(X, h0, c0, parameters)
    l = loss(H, Y)
    l.backward()
    opt.step()

训练一个多层LSTM也不难，可以选择先在深度或者时间维度上正向传播，再在另一个维度上正向传播。示例代码采用先时间再深度的形式：

1
2
3
4
5
6
7

def train_lstm(X, Y, h0, c0, parameters)
    H = X
    for i in range(depth):
        H, cn = lstm(H, h0[i], c0[i], parameters[i])
    l = loss(H, Y)
    l.backward()
    opt.step()

接下来重头戏来了。如果我们的序列长度很长，那么进行一次正向传播需要保存的中间变量就很多很多，显存可能不够，怎么解决这个问题？

我们可以把这个序列按照某个固定长度进行截断，首先计算第一段中的loss，并进行反向传播，然后对后一段继续进行正向传播，同时将第一段的最后一个cell state作为第二段的初始state传入，然后反向传播…

一直等到整个序列处理完毕，再更新参数。理解这个过程后，不难发现，阶段版本和完整版本是完全等价的，这也是为什么lstm需要返回最后一个cell state。上述过程可描述为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

def train_lstm(X, Y, h0, c0, parameters)
    H, cn = lstm(X, h0, c0, parameters)
    l = loss(H, Y)
    l.backward()
    opt.step()
    return H[-1].data, cn.data

h0, c0 = zeros()
for i in range(0,X.shape[0],BLOCK_SIZE):
    h0, c0 = train_lstm(X[i:i+BLOCK_SIZE], Y[i:i+BLOCK_SIZE], h0, c0, parameters)

Lecture 20: Transformers and Attention

两种为时间序列建模的方法 The two approaches to time series modeling

RNN在对时间序列建模时采用了一种被称为潜在状态latent state的方式，具体来说，其使用t时刻的hidden state来描述t及t时刻往前的所有信息。这种方法的优点是其理论上可以聚合无限长时刻的信息，缺点是其难以有效记住较远时刻的信息，并且存在梯度爆炸和消失问题。

而另一种建模方式被称为直接预测 direct prediction，具体来说，直接使用t和t时刻之前的sequence来预测t时刻的输出。这种方式的优点时，对于大部分输出，其计算路径要短的，缺点是没有明确的状态表示，在实践中往往序列长度有限。Transformer就属于这种直接预测方式对时间序列进行建模。

【此处跳过对CNN用于时间序列建模及其优缺点的介绍】

自注意力机制和Transformer Self-attention and transformers

Attention机制本质上指的是任何对状态进行加权求和的机制，这个权重显然不应该由我们自己决定，而是可学习的参数，再经过一层softmax后得到的权重。

而自注意力机制，顾名思义，就是由状态自己来决定权重，然后对状态按权重求和的机制。

在自注意力中，KQV是三个shape相同的矩阵，即$K,Q,V\in \mathbb{R}^{T\times d}$ ，KQV都是由输入$X$乘上不同的权重得到的$W_K W_Q W_V$得到，self-attention算子的定义为：

$$ \text{SelfAttention}(K,Q,V) = \text{softmax}(\frac{KQ^T}{\sqrt{d}})V $$
其中，softmax操作是对每一行进行的。

接下来我们尝试理解这个式子在做什么。首先我们要明确，KQV的每一行都是由X对应行加权求和得到的，也就是说，KQV每一行并没有其它行的时序信息（X的每一行表示一个时间的输入）。$KQ^T$是一个T×T的矩阵，其第i行第j个元素是由K的第i行和j的第i列作内积得到，在这里，时序信息进行了交换。对于$KQ^T$的第i行，其每个元素的值大小在一定程度上反应了Q中每一列与之的相似度，然后对这一行进行了softmax操作，得到权重。接下来将这个权重矩阵乘上V，得到自注意力的值。最后得到的结果矩阵中，每一行结果都是根据权重矩阵对V进行加权求和得到的，也正是在这里，发生了时序信息的混合。

自注意力有如下几个特点

  • 对KQV的排列具有不变性（实际上是等价性）。也就是说，如果按行重排KQV，自注意力的结果不会因此改变，只会因此发生对应的重排。
  • 自注意力机制会在所有的时间步上起作用，也就是自注意力可以混合时序信息。
  • 计算开销为$O(T^2d)$。

一个Transformer Block结构如下图所示： image.png

这个流程用公式表示为：

$$ \begin{align*} \tilde{Z} &:= \text{SelfAttention}\big(Z^{(i)}W_K,Z^{(i)}W_Q,Z^{(i)}W_V\big) \\ &= \mathrm{softmax}\left(\frac{Z^{(i)}W_KW_V^T(Z^{(i)})^T}{d^{1/2}}\right)Z^{(i)}W_V \\ \tilde{Z} &:= \text{LayerNorm}\bigg(Z^{(i)} \boldsymbol{+}\tilde{Z}\bigg) \\ Z^{(i+1)} &:= \text{LayerNorm}(\mathrm{ReLU}(\tilde{Z}W)+\tilde{Z}) \end{align*} $$

Transformer的优点是：

  • 可以在一个block中混合所有时间步的时序信息；
  • 随着时间步的增加，Transformer不需要额外引入新的参数。

其缺点是：

  • 每个输出都依赖于所有时间步的输入；
  • 输入没有时序，也就是说可以将时序打乱再输入给Transformer，结果还是一样的。

接下来介绍两种技术针对缺点进行改进。

首先是掩码自注意力，即masked self-attention。之前提到，在自注意力的计算公式中，softmax后的$KQ^T$是一个密集矩阵，每一行都是表示一个权重，会将所有时刻的状态加权求和。而掩码自注意力的做法是，将让$KQ^T$的上三角部分减去无穷大，这样权重矩阵的上三角部分为0，即只对t之前的时刻加权求和，以防止获取未来信息。

为了解决输入时序的问题，引入了位置编码position encoding技术，给输入加上一个用于表示时间信息的矩阵，如下所示：

$$ X\in\mathbb{R}^n= \begin{bmatrix}-&x_1^\top&-\\-&x_2^\top&-\\&\vdots&\\-&x_T^\top&-\end{bmatrix}+\begin{bmatrix}\sin(\omega_1\cdot1)&\cdots&\sin(\omega_n\cdot1)\\\sin(\omega_1\cdot2)&\cdots&\sin(\omega_n\cdot2)\\\vdots&\ddots&\vdots\\\sin(\omega_1\cdot T)&\cdots&\sin(\omega_n\cdot T)\end{bmatrix} $$
通常，其中的$w_i$根据对数函数的变化趋势来选择。

Lecture 21: Transformer Implementation

本节课中，我们将使用NumPy来实现Transformer。

自注意力机制 Self-attention

自注意力的公式为：

$$ Y = \left(\mathrm{softmax}\left(\frac{X W_K W_Q^T X^T}{\sqrt{d}}\right)X W_V \right) W_o $$
与上一讲有些许不同之处在于在输出前进行了一次额外的线性变换。

注意到公式中我们需要将X与三个W分别相乘以得到KQV，可以将这三次矩阵运算变为一个运算，即将三个矩阵concat在一起，然后与X相乘，一下子得到concat在一起的KQV。一个自注意力模块为：

1
2
3
4

def self_attention(X, mask, W_KQV, W_out):
    K,Q,V = np.split(X@W_KQV, 3, axis=-1)
    attn = softmax(K@Q.swapaxes(-1,-2) / np.sqrt(X.shape[-1]) + mask)
    return attn@V@W_out, attn

Minibatching with batch matrix multiply

自注意力不是按照时间循序进行前向传播的，因此X仍按照正常BTD的顺序在内存中组织。当我们实现批量self-attention时，就涉及到了批量矩阵乘法的概念。

具体来说，公式中$K@Q^T$这一步的矩阵乘法，K和Q的shape都是B×T×T，这就涉及到了批量矩阵乘法。对我们都自注意力来说，想要的应该是K[i,:,:]与Q.T[i,:,:]相乘，碰巧，批量矩阵乘法正是这么定义的，也就是说，批量矩阵乘法要求两个矩阵之间除了倒数两个维度符合矩阵乘法要求，剩余其它维度要么不存在或为1进行广播，要么就是要相等的。

Multihead attention 多头注意力

多头自注意力的动机来自于$K@Q^T$这一步，结果每个元素都是长度为d的两个向量内积得到的。为了降低计算成本，提出了一种多头注意力机制。即，将KQV的每一行分为h个部分，进行注意力操作，然后再拼接起来。这样，$K@Q^T$每个值都是长度为d/h向量进行内积得到的。

1
2
3
4
5
6
7

def multihead_attention(X, mask, heads, W_KQV, W_out):
    N,T,d = X.shape
    K,Q,V = np.split(X@W_KQV, 3, axis=-1)
    K,Q,V = [a.reshape(N,T,heads,d//heads).swapaxes(1,2) for a in (K,Q,V)]
    
    attn = softmax(K@Q.swapaxes(-1,-2) / np.sqrt(d//heads) + mask)
    return (attn@V).swapaxes(1,2).reshape(N,T,d) @ W_out, attn

Transformer block

一个Transformer Block结构如下图所示： image.png

应用已经实现的各个组件，我们可以轻松地写出一个支持多头自注意力的Transformer块：

1
2
3
4
5
6
7
8
9

def layer_norm(Z, eps):
    return (Z - Z.mean(axis=-1, keepdims=True)) / np.sqrt(Z.var(axis=-1, keepdims=True) + eps)
    
def relu(Z):
    return np.maximum(Z,0)

def transformer(X, mask, heads, W_KQV, W_out, W_ff1, W_ff2, eps):
    Z = layer_norm(multihead_attention(X, mask, heads, W_KQV, W_out)[0] + X, eps)
    return layer_norm(Z + relu(Z@W_ff1)@W_ff2, eps)

Lecture 23 Moel Deployment

模型部署概览 Model deployment overview

在特定的设备上部署训练好的模型是一件比较麻烦的事情，其受设备的影响很大。现在有一些用于部署推理的框架，例如NVIDIA设备上的TensorRT，在嵌入式设备上有ARMComputeLib和TFLite，苹果有CoreML。

上述框架都需要一种推理模型格式的输入，这个输入能够描述模型的计算流程，这种格式目前有ONNX、CoreML和TFLite。模型通过Python编写，其好处是提高了编码效率，带来的缺点就是可能某些模型没办法完美转换为上述通用格式。

许多推理框架都是以计算图解释器的形式组织的，其通过预分配和重用内存、算子融合、精度量化等优化手段，实现更高效的推理。但同样，其也有很多限制，例如他们支持的算子类别是有限的。

机器学习编译 Machine learning compilation

机器学习编译试图打破需要为每种设备定制推理库的现状，其目标是将输入的深度学习模型转换为可以直接在终端上运行的代码。

一个ML程序可以被称为一个模块，这个模块由多个函数构成，函数之间互相调用。下图这种格式被称为中间状态表示IR，下图这一模块被称为IR模块。

image.png

ML编译的流程大致有：

  • 从深度学习框架中导入模型；

  • 对IR模块进行变换，算子融合 image.png

  • 将中间状态翻译为更低级的循环代码 image.png

  • 进行更低级的变换，进行算子融合 image.png

  • 进行代码生成 image.png 本讲后续内容和下一讲均为介绍MLC，计划后面继续学习MLC，这里就不浅尝辄止了。

全文完。

参考文档

  1. 指数移动平均EMA_ema移动平均数怎么算-CSDN博客 ↩︎

  2. zhuanlan.zhihu.com/p/22810533 ↩︎

  3. An overview of gradient descent optimization algorithms ↩︎

  4. numpy.lib.stride_tricks.as_strided — NumPy v2.1 Manual ↩︎